2018年センター試験 数学ⅠA 第2問 三角比の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
2018年 センターⅠA 第2問 三角比 四角形ABCDにおいて,3辺の長さをそれぞれ $\mathrm{AB}=5$, $\mathrm{BC}=9$, $\mathrm{CD}=3$,
対角線ACの長さを $\mathrm{AC}=6$ とする。このとき
ここで,四角形ABCDは台形であるとする。
次の $\mybox{カ}$ には下の⓪~②から,$\mybox{キ}$ には③・④から当てはまるものを一つずつ選べ。
$\mathrm{CD}~\myBox{カ}~\mathrm{AB}\Cdot\sin\kaku{ABC}$ であるから $\myBox{キ}$ である。
⓪ $<$ ① $=$ ② $>$
③ 辺ADと辺BCが平行 ④ 辺ABと辺CDが平行
したがって
対角線ACの長さを $\mathrm{AC}=6$ とする。このとき
\begin{align*}
\cos\kaku{ABC}=\dfrac{\myBox{ア}}{\myBox{イ}},~\sin\kaku{ABC}=\dfrac{\myBox{ウ}\sqrt{\myBox{エ}}}{\myBox{オ}}
\end{align*}
である。\cos\kaku{ABC}=\dfrac{\myBox{ア}}{\myBox{イ}},~\sin\kaku{ABC}=\dfrac{\myBox{ウ}\sqrt{\myBox{エ}}}{\myBox{オ}}
\end{align*}
ここで,四角形ABCDは台形であるとする。
次の $\mybox{カ}$ には下の⓪~②から,$\mybox{キ}$ には③・④から当てはまるものを一つずつ選べ。
$\mathrm{CD}~\myBox{カ}~\mathrm{AB}\Cdot\sin\kaku{ABC}$ であるから $\myBox{キ}$ である。
⓪ $<$ ① $=$ ② $>$
③ 辺ADと辺BCが平行 ④ 辺ABと辺CDが平行
したがって
\begin{align*}
\mathrm{BD}=\myBox{ク}\sqrt{\myBox{ケコ}}
\end{align*}
である。\mathrm{BD}=\myBox{ク}\sqrt{\myBox{ケコ}}
\end{align*}
考え方と解答

ヒロ
3辺の長さから $\cos$ の値を求める問題だから,サクサク計算していこう。
【アイの解答】
余弦定理より
余弦定理より
\begin{align*}
\cos\kaku{ABC}&=\dfrac{5^2+9^2-6^2}{2\Cdota5\Cdota9} \\[4pt]
&=\dfrac{25+81-36}{90} \\[4pt]
&=\dfrac{70}{90}=\dfrac{7}{9}
\end{align*}
\cos\kaku{ABC}&=\dfrac{5^2+9^2-6^2}{2\Cdota5\Cdota9} \\[4pt]
&=\dfrac{25+81-36}{90} \\[4pt]
&=\dfrac{70}{90}=\dfrac{7}{9}
\end{align*}

ヒロ
次は $\cos$ から $\sin$ の値を求める問題。
【ウ~オの解答】
$\sin\kaku{ABC}>0$ より
$\sin\kaku{ABC}>0$ より
\begin{align*}
\sin\kaku{ABC}&=\sqrt{1-\cos^2B} \\[4pt]
&=\sqrt{1-\left(\dfrac{7}{9}\right)^2} \\[4pt]
&=\dfrac{4\sqrt{2}}{9}
\end{align*}
\sin\kaku{ABC}&=\sqrt{1-\cos^2B} \\[4pt]
&=\sqrt{1-\left(\dfrac{7}{9}\right)^2} \\[4pt]
&=\dfrac{4\sqrt{2}}{9}
\end{align*}

ヒロ
次は値の大小比較の問題。
【カの解答】
\begin{align*}
&\mathrm{CD}=3 \\[4pt]
&\mathrm{AB}\sin\kaku{ABC}=5\Cdota\dfrac{4\sqrt{2}}{9}=\dfrac{20\sqrt{2}}{9}
\end{align*}
$20\sqrt{2}>20\times1.4=28$ であるから,$\mathrm{CD}<\mathrm{AB}\sin\kaku{ABC}$ となる。 よって,$\myBox{カ}=⓪$&\mathrm{CD}=3 \\[4pt]
&\mathrm{AB}\sin\kaku{ABC}=5\Cdota\dfrac{4\sqrt{2}}{9}=\dfrac{20\sqrt{2}}{9}
\end{align*}

ヒロ
CDと $\mathrm{AB}\sin B$ の大小関係から,どの2辺が平行かを判断する問題。
【キの解答】 四角形ABCEが平行四辺形になるように点Eをとると,次のようになる。
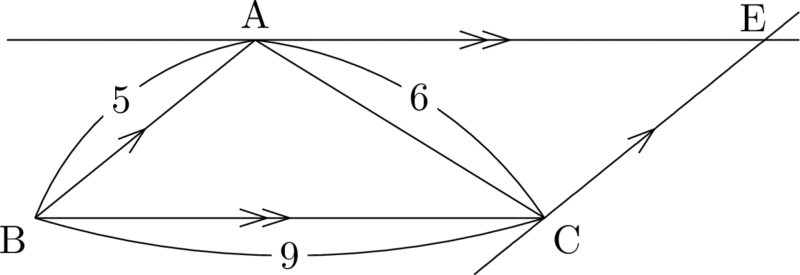
四角形ABCDは台形であるから,点DはAE上かCE上のどちらかにある。 ここで,$\mathrm{AB}\sin B$ が点Aから辺BCに下ろした垂線AHの長さを表していることを考えよう。 そして,先ほどの計算から,垂線AHの長さがCDより長いことが分かっている。 したがって,辺AE上に点Dをとろうと思ってもとることができない。次の図では,理解の手助けとして,点Cを中心とする半径3の円を描いた。円と辺AEが共有点をもたないことを次の図で確認しよう。つまり,点Dは辺CE上にある。
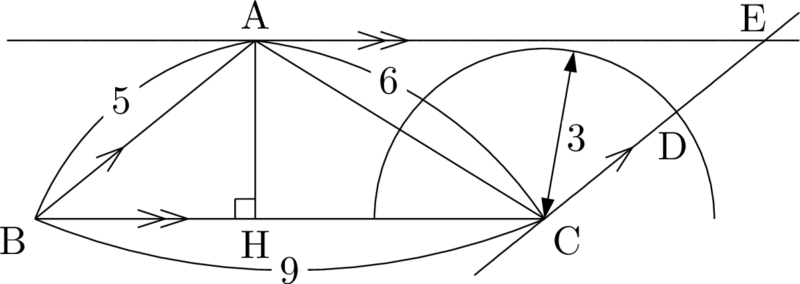
よって,辺ABと辺CDが平行である。$\myBox{キ}=④$

四角形ABCDは台形であるから,点DはAE上かCE上のどちらかにある。 ここで,$\mathrm{AB}\sin B$ が点Aから辺BCに下ろした垂線AHの長さを表していることを考えよう。 そして,先ほどの計算から,垂線AHの長さがCDより長いことが分かっている。 したがって,辺AE上に点Dをとろうと思ってもとることができない。次の図では,理解の手助けとして,点Cを中心とする半径3の円を描いた。円と辺AEが共有点をもたないことを次の図で確認しよう。つまり,点Dは辺CE上にある。

よって,辺ABと辺CDが平行である。$\myBox{キ}=④$

ヒロ
最後はBDの長さを求める問題。
【ク~コの解答】 $\sankaku{BCD}$ に着目して余弦定理でBDを求めよう。
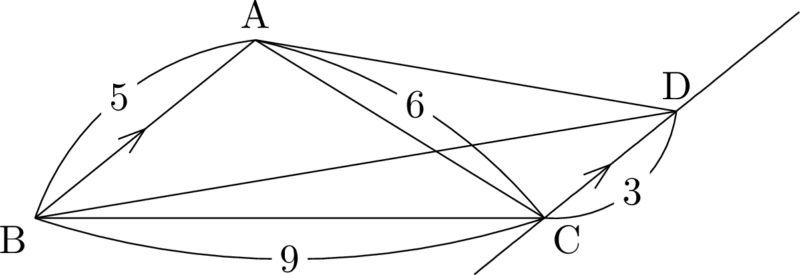
$\kaku{BCD}=180\Deg-\kaku{ABC}$ であるから

$\kaku{BCD}=180\Deg-\kaku{ABC}$ であるから
\begin{align*} \cos\kaku{BCD}&=\cos(180\Deg-\kaku{ABC}) \\[4pt] &=-\cos\kaku{ABC} \\[4pt] &=-\dfrac{7}{9}
\end{align*}
よって,$\sankaku{BCD}$ において余弦定理より\end{align*}
\begin{align*} \mathrm{BD}^2&=9^2+3^2-2\Cdota9\Cdota3\Cdota\left(-\dfrac{7}{9}\right) \\[4pt] &=90+42=132
\end{align*}
$\mathrm{BD}>0$ より\end{align*}
\begin{align*}
\mathrm{BD}=\sqrt{132}=2\sqrt{33}
\end{align*}
\mathrm{BD}=\sqrt{132}=2\sqrt{33}
\end{align*}
2018年 センター数学ⅠA 三角比を解いた感想

ヒロ
問題を見たときに「どの公式を使うんだろう?」と最初に考える人だと,$\myBox{キ}$ 以降は解けないだろう。

ヒロ
$\myBox{キ}$ を素早く求めるためには,三角比の値と図形との関係をよく理解していることが重要である。

ヒロ
$\myBox{キ}$ が分かれば,BDの長さはボーナス問題になるので,得点差が大きくなる。




















