2017年のセンター試験 数学ⅡB 第4問ベクトルの解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
(1) 点Bの座標は $\left(\myBox{ア},~\sqrt{\myBox{イ}}\right)$,点Dの座標は $\left(-\myBox{ウ},~0\right)$ である。
(2) 線分BDの中点をMとし,直線AMと直線CDの交点をNとする。$\Vec{ON}$ を求めよう。
$\Vec{ON}$ は実数 $r,~s$ を用いて,$\Vec{ON}=\Vec{OA}+r\Vec{AM}$, $\Vec{ON}=\Vec{OD}+s\Vec{DC}$
と2通りに表すことができる。ここで
&\Vec{AM}=\left(-\dfrac{\myBox{エ}}{\myBox{オ}},~\dfrac{\sqrt{\myBox{カ}}}{\myBox{キ}}\right) \\[4pt]
&\Vec{DC}=\left(\myBox{ク},~\sqrt{\myBox{ケ}}\right)
\end{align*}
であるから
r=\dfrac{\myBox{コ}}{\myBox{サ}},~s=\dfrac{\myBox{シ}}{\myBox{ス}}
\end{align*}
\Vec{ON}=\left(-\dfrac{\myBox{セ}}{\myBox{ソ}},~\dfrac{\myBox{タ}\sqrt{\myBox{チ}}}{\myBox{ツ}}\right)
\end{align*}
(3) 線分BF上に点Pをとり,その $y$ 座標を $a$ とする。点Pから直線CEに引いた垂線と,点Cから直線EPに引いた垂線との交点をHとする。
$\Vec{EP}$が
\Vec{EP}=\left(\myBox{テ},~\myBox{ト}+\sqrt{\myBox{ナ}}\right)
\end{align*}
\left(\dfrac{\myBox{ニ}~a^{\myBox{ヌ}}+\myBox{ネ}}{\myBox{ノ}},~\myBox{ハ}\right)
\end{align*}
さらに,$\Vec{OP}$ と $\Vec{OH}$ のなす角を $\theta$ とする。$\cos\theta=\dfrac{12}{13}$のとき,$a$の値は
a=\pm\dfrac{\myBox{ヒ}}{\myBox{フヘ}}
\end{align*}
(1)の解答

まずは正六角形を描いて状況を把握しよう。
問題文に合うように図を描くと次のようになる。
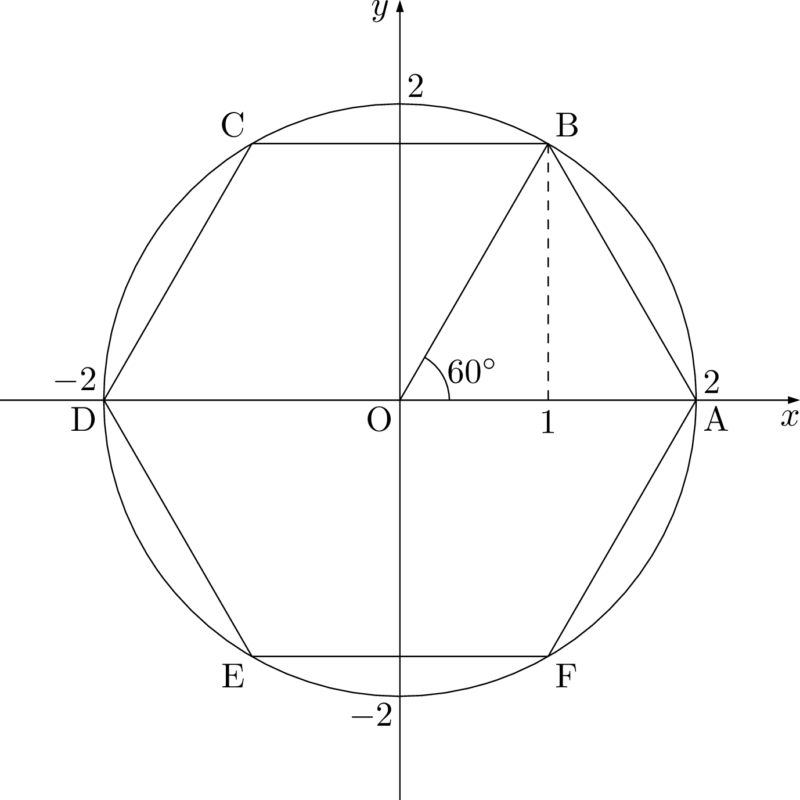
図より,点Bの座標は $(1,~\sqrt3)$,点Dの座標は $(-2,~0)$ と分かる。
(2)の解答

まずは $\Vec{AM}$ と $\Vec{DC}$ の成分を求めよう。
MはBDの中点だから
\Vec{AM}
&=\Vec{OM}-\Vec{OA} \\[4pt]
&=\dfrac12(\Vec{OB}+\Vec{OD})-\Vec{OA} \\[4pt]
&=\dfrac{1}{2}\Vec{OC}-\Vec{OA} \\[4pt]
&=\dfrac12(-1,~\sqrt3)-(2,~0) \\[4pt]
&=\left(-\dfrac{5}{2},~\dfrac{\sqrt3}{2}\right) \\[4pt]
\Vec{DC}&=\Vec{OB} \\[4pt]
&=(1,~\sqrt3)
\end{align*}

四角形OBCDがひし形であることが瞬時に分かれば,$\Vec{DC}=\Vec{OB}$ となるから楽に成分を求めることができる。

次は,$r$ と $s$ の値を求める問題。$\Vec{ON}$ が2通りに表されていることを利用しよう。
\Vec{ON}&=\Vec{OA}+r\Vec{AM} \\[4pt]
&=(2,~0)+r\left(-\dfrac{5}{2},~\dfrac{\sqrt3}{2}\right) \\[4pt]
&=\left(-\dfrac{5}{2}r+2,~\dfrac{\sqrt3}{2}r\right)
\end{align*}
\Vec{ON}&=\Vec{OD}+s\Vec{DC} \\[4pt]
&=(-2,~0)+s(1,~\sqrt3) \\[4pt]
&=(s-2,~\sqrt3s)
\end{align*}
&\begin{cases}
-\dfrac{5}{2}r+2=s-2 &\cdots\cdots① \\[4pt]
\dfrac{\sqrt3}{2}r=\sqrt3s &\cdots\cdots②
\end{cases}
\end{align*}
①に代入して
&-5s+2=s-2 \\[4pt]
&s=\dfrac{2}{3}
\end{align*}

$r,~s$ の値が求まったので,$\Vec{ON}$ の成分も分かる。今回は $s$ を使う方が楽だね。
\Vec{ON}&=\left(\dfrac{2}{3}-2,~\dfrac{2\sqrt3}{3}\right) \\[4pt]
&=\left(-\dfrac{4}{3},~\dfrac{2\sqrt3}{3}\right)
\end{align*}
(3)の解答

図を描かずに $\Vec{EP}$ を求められる人はそのまま図を描かずに求めよう。

そうでない人は図を描いて状況を把握しよう。
点Pの位置を確認すると,次の図のようになる。
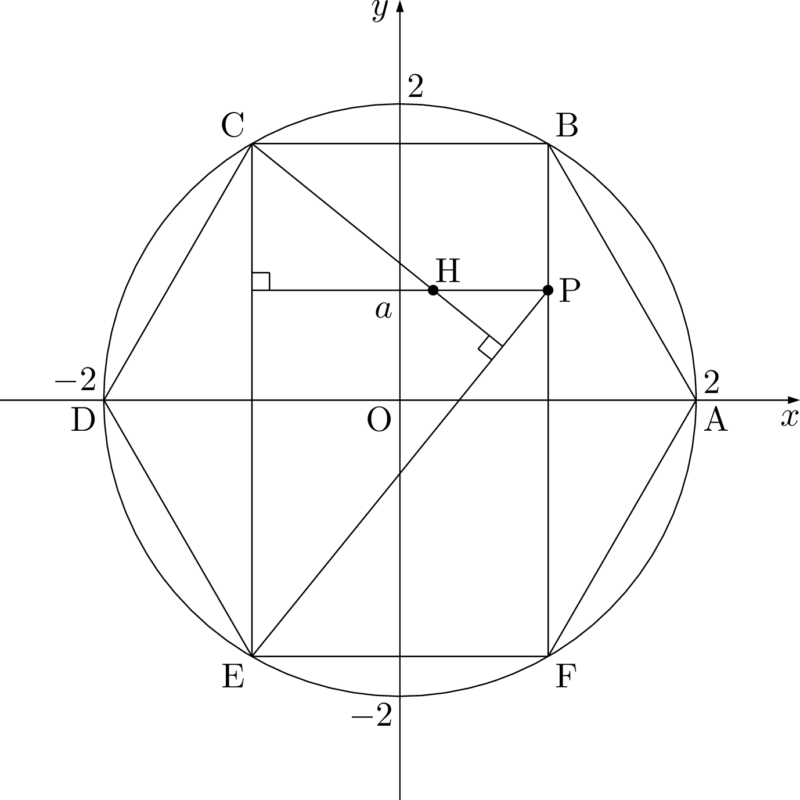
図より,$\mathrm{P}(1,~a)$, $\mathrm{E}(-1,~-\sqrt3)$ であるから
\Vec{EP}&=\Vec{OP}-\Vec{OE} \\[4pt]
&=(2,~a+\sqrt3)
\end{align*}

次のHの座標を求めよう。

PからCEに引いた垂線とCからEPに引いた垂線の交点がHだから,この情報をどう扱うかが重要。

まず,すぐに分かるのは $\myBox{ハ}$。HはPからCEに引いた垂線上にあるから,Hの $y$ 座標は $a$ と分かる。

問題は $x$ 座標。これはHがCからEPに引いた垂線上にあることを利用しないといけない。

垂直な方向をサクッと作れるかどうかがポイントだね。直前に $\Vec{EP}$ の成分を求めているので,これを利用して $\Vec{CH}$ を1つの文字を使って表そう。

文字が1つだけなら,$y$ 成分が $a$ であることから,その文字を簡単に求めることができるね。
$\Vec{EP}=(2,~a+\sqrt3)$ より,$\Vec{CH}=t(a+\sqrt3,~-2)~(t>0)$ とおけるから
\Vec{OH}&=\Vec{OC}+\Vec{CH} \\[4pt]
&=(-1,~\sqrt3)+t(a+\sqrt3,~-2) \\[4pt]
&=(-1+t(a+\sqrt3),~\sqrt3-2t)
\end{align*}
&\sqrt3-2t=a \\[4pt]
&t=\dfrac{\sqrt3-a}{2}
\end{align*}
&-1+\dfrac{\sqrt3-a}{2}(a+\sqrt3) \\[4pt]
&=-1+\dfrac{3-a^2}{2} \\[4pt]
&=\dfrac{1-a^2}{2}
\end{align*}
\left(\dfrac{-a^2+1}{2},~a\right)
\end{align*}

最後は余弦の値から $a$ の値を求める問題。内積を利用するのは言うまでもないだろう。
$\mathrm{P}(1,~a)$, $\mathrm{H}\left(\dfrac{-a^2+1}{2},~a\right)$ より
\Vec{OP}\Cdot\Vec{OH}&=\dfrac{-a^2+1}{2}+a^2 \\[4pt]
&=\dfrac{a^2+1}{2}
\end{align*}
\abs{\Vec{OP}}&=\sqrt{a^2+1} \\[4pt]
\abs{\Vec{OH}}&=\sqrt{\left(\dfrac{-a^2+1}{2}\right)^2+a^2} \\[4pt]
&=\sqrt{\dfrac{a^4+2a^2+1}{4}} \\[4pt]
&=\sqrt{\left(\dfrac{a^2+1}{2}\right)^2} \\[4pt]
&=\abs{\dfrac{a^2+1}{2}} \\[4pt]
&=\dfrac{a^2+1}{2}
\end{align*}
&\dfrac{\dfrac{a^2+1}{2}}{\sqrt{a^2+1}\Cdot\dfrac{a^2+1}{2}}=\dfrac{12}{13} \\[4pt]
&\dfrac{1}{\sqrt{a^2+1}}=\dfrac{12}{13} \\[4pt]
&\sqrt{a^2+1}=\dfrac{13}{12} \\[4pt]
&a^2+1=\left(\dfrac{13}{12}\right)^2 \\[4pt]
&a^2=\left(\dfrac{13}{12}\right)^2-1 \\[4pt]
&a^2=\left(\dfrac{5}{12}\right)^2 \\[4pt]
&a=\pm\dfrac{5}{12}
\end{align*}
2017年 センター数学ⅡB ベクトルを解いた感想

円に内接する正六角形が扱われているため,最初に図を描いた方が考えやすいだろう。

最後の方の問題では,計算は面倒であるが,問われていること自体はそれほど難しいものではないだろう。

日頃から標準レベルの問題を解いていくことが重要である。




















