1999年センター試験 数学ⅡB 第1問 複素数平面の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
1999年 センターⅡB 第1問 複素数平面 実数係数の方程式
①の解を $2,~\alpha,~\beta$ とし,複素数平面において3点 2, $\alpha$, $\beta$ が正方形の異なる三つの頂点になっているとする。さらに,この正方形の一辺の長さが $5\sqrt{2}$ で,$\alpha$, $\beta$ の実部が負であるならば,$\alpha$, $\beta$ は
\begin{align*}
x^3+ax^2+bx+c=0~\cdots\cdots①
\end{align*}
が $x=2$ を解にもつとする。このときx^3+ax^2+bx+c=0~\cdots\cdots①
\end{align*}
\begin{align*}
c=-\myBox{ア}\,a-\myBox{イ}\,b-\myBox{ウ}
\end{align*}
でありc=-\myBox{ア}\,a-\myBox{イ}\,b-\myBox{ウ}
\end{align*}
\begin{align*}
&x^3+ax^2+bx+c \\[4pt]
&=(x-2)\left\{x^2+\left(a+\myBox{エ}\right)x+\myBox{オ}\,a+b+\myBox{カ}\right\}
\end{align*}
となる。&x^3+ax^2+bx+c \\[4pt]
&=(x-2)\left\{x^2+\left(a+\myBox{エ}\right)x+\myBox{オ}\,a+b+\myBox{カ}\right\}
\end{align*}
①の解を $2,~\alpha,~\beta$ とし,複素数平面において3点 2, $\alpha$, $\beta$ が正方形の異なる三つの頂点になっているとする。さらに,この正方形の一辺の長さが $5\sqrt{2}$ で,$\alpha$, $\beta$ の実部が負であるならば,$\alpha$, $\beta$ は
\begin{align*}
\myBox{キク}\pm\myBox{ケ}\,i
\end{align*}
である。このとき\myBox{キク}\pm\myBox{ケ}\,i
\end{align*}
\begin{align*}
a=\myBox{コ},~b=\myBox{サシ},~c=\myBox{スセソ}
\end{align*}
となる。a=\myBox{コ},~b=\myBox{サシ},~c=\myBox{スセソ}
\end{align*}
考え方と解答

ヒロ
$x=2$ が解である意味を考えよう。
方程式の解とは$x$ の方程式 $f(x)=0$ が $x=a$ を解にもつとき
\begin{align*}
f(a)=0
\end{align*}
が成り立つ。f(a)=0
\end{align*}
【ア~ウの解答】
$x=2$ が①の解であるから
$x=2$ が①の解であるから
\begin{align*}
&8+4a+2b+c=0 \\[4pt]
&c=-4a-2b-8
\end{align*}
&8+4a+2b+c=0 \\[4pt]
&c=-4a-2b-8
\end{align*}

ヒロ
次は3次式を因数分解する問題。

ヒロ
$x=2$ が①の解であることから,因数定理より,①の左辺が $x-2$ を因数にもつことが分かるから割り算をしよう。
因数定理$x$ の多項式 $f(x)$ について $f(a)=0$ が成り立つとき,$f(x)$ は $x-a$ を因数にもつ。

ヒロ
割り算をする方法は,筆算・組立除法・暗算の3通りある。

ヒロ
より速く割り算ができる方法を身に付けよう。
【エ~カの解答】
\begin{align*}
&x^3+ax^2+bx+c \\[4pt]
&=x^3+ax^2+bx-4a-2b-8 \\[4pt]
&=(x-2)\{x^2+(a+2)x+2a+b+4\}
\end{align*}
&x^3+ax^2+bx+c \\[4pt]
&=x^3+ax^2+bx-4a-2b-8 \\[4pt]
&=(x-2)\{x^2+(a+2)x+2a+b+4\}
\end{align*}

ヒロ
暗算で割り算をすると,上のようにどのように考えた結果なのかが見た人には伝わらない。

ヒロ
ただ,割り算程度で考えも糞もないので,記述式試験であっても上のように書いても減点されない。

ヒロ
暗算ができない人は,次のように文字に着目する方法もアリだろう。

ヒロ
文字に関係ない $x-2$ が因数としてくくれることが分かっているから,それぞれの文字に着目するとうまくいくはず。
【エ~カの別解】
\begin{align*}
&x^3+ax^2+bx+c \\[4pt]
&=x^3+ax^2+bx-4a-2b-8 \\[4pt]
&=(x^3-8)+a(x^2-4)+b(x-2) \\[4pt]
&=(x-2)(x^2+2x+4)+a(x-2)(x+2)+b(x-2) \\[4pt]
&=(x-2)\{(x^2+2x+4)+a(x+2)+b\} \\[4pt]
&=(x-2)\{x^2+(a+2)x+2a+b+4\}
\end{align*}
&x^3+ax^2+bx+c \\[4pt]
&=x^3+ax^2+bx-4a-2b-8 \\[4pt]
&=(x^3-8)+a(x^2-4)+b(x-2) \\[4pt]
&=(x-2)(x^2+2x+4)+a(x-2)(x+2)+b(x-2) \\[4pt]
&=(x-2)\{(x^2+2x+4)+a(x+2)+b\} \\[4pt]
&=(x-2)\{x^2+(a+2)x+2a+b+4\}
\end{align*}

ヒロ
次は正方形の頂点を求める問題。
【$2,~\alpha,~\beta$ の位置を把握する】
①の解が $2,~\alpha,~\beta$ であるから,$\alpha,~\beta$ は
\begin{align*}
x^2+(a+2)x+2a+b+4=0
\end{align*}
の2解である。つまり,$\alpha,~\beta$ の実部が等しいから,複素数平面上で $\alpha,~\beta$ は実軸に対称で,縦に並ぶ。x^2+(a+2)x+2a+b+4=0
\end{align*}
さらに,$\alpha,~\beta$ の実部が負であることから,題意の正方形は次のようになっていることが分かる。
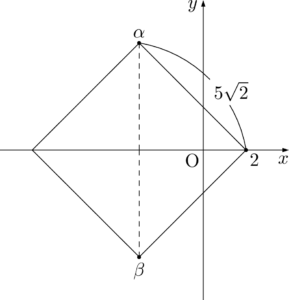
【キ~ケの解答】
上のように考えて図を描くと,$\alpha$ の虚部が5であることが分かるから,次の図のようになる。
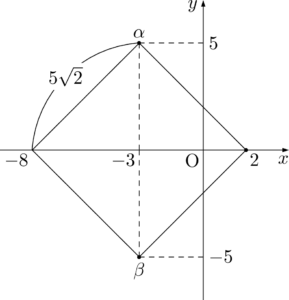
よって,$\alpha,~\beta$ は $-3\pm5i$ である。
上のように考えて図を描くと,$\alpha$ の虚部が5であることが分かるから,次の図のようになる。

よって,$\alpha,~\beta$ は $-3\pm5i$ である。

ヒロ
最後は $a,~b,~c$ の値を求める問題。

ヒロ
2次方程式の2解が分かっているから,解と係数の関係を利用すれば係数を求めることができるね。
2次方程式の2解が分かっているとき2解が $p,~q$ となるような2次方程式の1つは
\begin{align*}
x^2-(p+q)x+pq=0
\end{align*}
である。x^2-(p+q)x+pq=0
\end{align*}
【コ~ソの解答】
$x^2+(a+2)x+2a+b+4=0$ の2解が $-3\pm5i$ であるから
$x^2+(a+2)x+2a+b+4=0$ の2解が $-3\pm5i$ であるから
\begin{align*}
&\begin{cases}
a+2=-\{(-3+5i)+(-3-5i)\} \\[4pt]
2a+b+4=(-3+5i)(-3-5i)
\end{cases}\\[4pt]
&\begin{cases}
a+2=6 \\[4pt]
2a+b+4=34
\end{cases}\\[4pt]
&a=4,~b=22
\end{align*}
3次方程式①の3つの解が $x=2,~-3\pm5i$ より&\begin{cases}
a+2=-\{(-3+5i)+(-3-5i)\} \\[4pt]
2a+b+4=(-3+5i)(-3-5i)
\end{cases}\\[4pt]
&\begin{cases}
a+2=6 \\[4pt]
2a+b+4=34
\end{cases}\\[4pt]
&a=4,~b=22
\end{align*}
\begin{align*}
c=-2(-3+5i)(-3-5i)=-68
\end{align*}
c=-2(-3+5i)(-3-5i)=-68
\end{align*}
1999年 センター数学ⅡB 複素数平面を解いた感想

ヒロ
前半は方程式の解の意味が分かっていて,3次式の因数分解をできるようにしておけば問題ないだろう。

ヒロ
後半は文章で書かれた内容を複素数平面上で図示できるかどうかがポイントとなる。

ヒロ
最後は解と係数の関係を理解していれば大丈夫。