ここでは三角比を含む方程式と不等式について説明します。
基本問題については次の記事で説明しています。
Contents
三角比を含む方程式の問題
問題$0\Deg\leqq\theta\leqq180\Deg$ とする。次の方程式を解け。
(1) $\sin\theta\tan\theta=-\dfrac{3}{2}$
(2) $\sqrt{2}\sin\theta=\tan\theta$
(1) $\sin\theta\tan\theta=-\dfrac{3}{2}$
(2) $\sqrt{2}\sin\theta=\tan\theta$
【(1)の考え方と解答】
$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ を利用して,方程式を $\sin\theta$ と $\cos\theta$ で表そう。
$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ を利用して,方程式を $\sin\theta$ と $\cos\theta$ で表そう。
\begin{align*}
&\sin\theta\Cdota\dfrac{\sin\theta}{\cos\theta}=-\dfrac{3}{2} \\[4pt]
&\sin^2\theta=-\dfrac{3}{2}\cos\theta
\end{align*}
次は $\cos\theta$ に統一しよう。&\sin\theta\Cdota\dfrac{\sin\theta}{\cos\theta}=-\dfrac{3}{2} \\[4pt]
&\sin^2\theta=-\dfrac{3}{2}\cos\theta
\end{align*}
\begin{align*}
&1-\cos^2\theta=-\dfrac{3}{2}\cos\theta \\[4pt]
&2\cos^2\theta-3\cos\theta-2=0 \\[4pt]
&(\cos\theta-2)(2\cos\theta+1)=0
\end{align*}
$0\Deg\leqq\theta\leqq180\Deg$ のとき $-1\leqq\cos\theta\leqq1$ であるから&1-\cos^2\theta=-\dfrac{3}{2}\cos\theta \\[4pt]
&2\cos^2\theta-3\cos\theta-2=0 \\[4pt]
&(\cos\theta-2)(2\cos\theta+1)=0
\end{align*}
\begin{align*}
&\cos\theta=-\dfrac{1}{2} \\[4pt]
&\theta=120\Deg
\end{align*}
&\cos\theta=-\dfrac{1}{2} \\[4pt]
&\theta=120\Deg
\end{align*}
(2) $\sqrt{2}\sin\theta=\tan\theta$
【(2)の考え方と解答】
$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ より
$\tan\theta=\dfrac{\sin\theta}{\cos\theta}$ より
\begin{align*}
&\sqrt{2}\sin\theta=\dfrac{\sin\theta}{\cos\theta} \\[4pt]
&\sqrt{2}\sin\theta\cos\theta=\sin\theta \\[4pt]
&\sin\theta(\sqrt{2}\cos\theta-1)=0 \\[4pt]
&\sin\theta=0,~\cos\theta=\dfrac{1}{\sqrt{2}}
\end{align*}
$0\Deg\leqq\theta\leqq180\Deg$ より,$\theta=0\Deg,~45\Deg,~180\Deg$&\sqrt{2}\sin\theta=\dfrac{\sin\theta}{\cos\theta} \\[4pt]
&\sqrt{2}\sin\theta\cos\theta=\sin\theta \\[4pt]
&\sin\theta(\sqrt{2}\cos\theta-1)=0 \\[4pt]
&\sin\theta=0,~\cos\theta=\dfrac{1}{\sqrt{2}}
\end{align*}
三角比を含む方程式・不等式の問題
問題$0\Deg\leqq\theta\leqq180\Deg$ のとき,次の方程式・不等式を解け。
(1) $2\cos^2\theta+5\sin\theta=4$
(2) $2\sin^2\theta+3\cos\theta<0$
(3) $\tan^2\theta+(1-\sqrt{3})\tan\theta-\sqrt{3}\leqq0$
(1) $2\cos^2\theta+5\sin\theta=4$
(2) $2\sin^2\theta+3\cos\theta<0$
(3) $\tan^2\theta+(1-\sqrt{3})\tan\theta-\sqrt{3}\leqq0$
【(1)の考え方と解答】 $\sin\theta$ と $\cos\theta$ が混在している方程式・不等式では,どちらか一方に統一できるかどうかを考えよう。$\sin^2\theta+\cos^2\theta=1$ を利用することで,$\sin^2\theta$ と $\cos^2\theta$ のどちらかをもう一方で表すことができる。 今回の場合は $\cos^2\theta=1-\sin^2\theta$ を利用して $\sin\theta$ に統一しよう。
よって,$\sin\theta=\dfrac{1}{2}$ $0\Deg\leqq\theta\leqq180\Deg$ であるから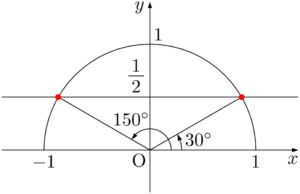
\begin{align*} &2(1-\sin^2\theta)+5\sin\theta=4 \\[4pt] &2\sin^2\theta-5\sin\theta+2=0 \end{align*}
$\sin\theta=t$ とおくと $t$ の2次方程式になるから $t$,すなわち $\sin\theta$ の値を求めることができる。その後,$\theta$ の値の範囲に注意して $\theta$ を求めよう。 $\sin\theta=t$ と置き換えずに書き進めることが苦でない人は $\sin\theta$ のまま書き進めよう。ここでは文字を置き換えて進めることにする。 $\sin\theta=t$ とおくと,$0\Deg\leqq\theta\leqq180\Deg$ のとき $-1\leqq t\leqq1$ である。 ※文字を置き換えた後は,定義域を考えるようにしよう。\begin{align*} &2t^2-5t+2=0 \\[4pt] &(t-2)(2t-1)=0 \\[4pt] &t=2,~\dfrac{1}{2} \end{align*}
$-1\leqq t\leqq1$ より,$t=\dfrac{1}{2}$よって,$\sin\theta=\dfrac{1}{2}$ $0\Deg\leqq\theta\leqq180\Deg$ であるから
\begin{align*} \theta=30\Deg,~150\Deg \end{align*}


ヒロ
因数分解のときのたすきがけが苦手な人は,次の記事からたすきがけのコツを知っておこう。

ヒロ
また $\sin\theta=t$ と置き換えずに $\sin\theta$ の値を求めた場合は $\sin\theta=2,~\dfrac{1}{2}$ となる。

ヒロ
ここで「$\sin\theta=2$ となる $\theta$ が分からない・・・」とならないようにしよう。

ヒロ
$\sin\theta$ は単位円周上の点の $y$ 座標であるから2にならないことがすぐに分かるようにしよう。
(2) $2\sin^2\theta+3\cos\theta<0$
【(2)の考え方と解答】
$\sin^2\theta$ と $\cos\theta$ が見えるから,$\sin^2\theta$ を $\cos\theta$ で表して $\cos\theta$ に統一しよう。 $\sin^2\theta=1-\cos^2\theta$ より
したがって,
$0\Deg\leqq\theta\leqq180\Deg$ より,$120\Deg<\theta\leqq180\Deg$
$\sin^2\theta$ と $\cos\theta$ が見えるから,$\sin^2\theta$ を $\cos\theta$ で表して $\cos\theta$ に統一しよう。 $\sin^2\theta=1-\cos^2\theta$ より
\begin{align*} &2(1-\cos^2\theta)+3\cos\theta<0 \\[4pt] &2\cos^2\theta-3\cos\theta-2>0 \\[4pt]
&(\cos\theta-2)(2\cos\theta+1)>0
\end{align*}
$0\Deg\leqq\theta\leqq180\Deg$ のとき $-1\leqq\cos\theta\leqq1$ であるから $\cos\theta-2<0$ である。&(\cos\theta-2)(2\cos\theta+1)>0
\end{align*}
したがって,
\begin{align*} &2\cos\theta+1<0 \\[4pt] &\cos\theta<-\dfrac{1}{2} \end{align*}

$0\Deg\leqq\theta\leqq180\Deg$ より,$120\Deg<\theta\leqq180\Deg$
(3) $\tan^2\theta+(1-\sqrt{3})\tan\theta-\sqrt{3}\leqq0$
【(3)の考え方と解答】
$\tan\theta=t$ とおくと $t$ の2次不等式になるね。ここでは文字を置き換えずに進めていこう。与えられた不等式より
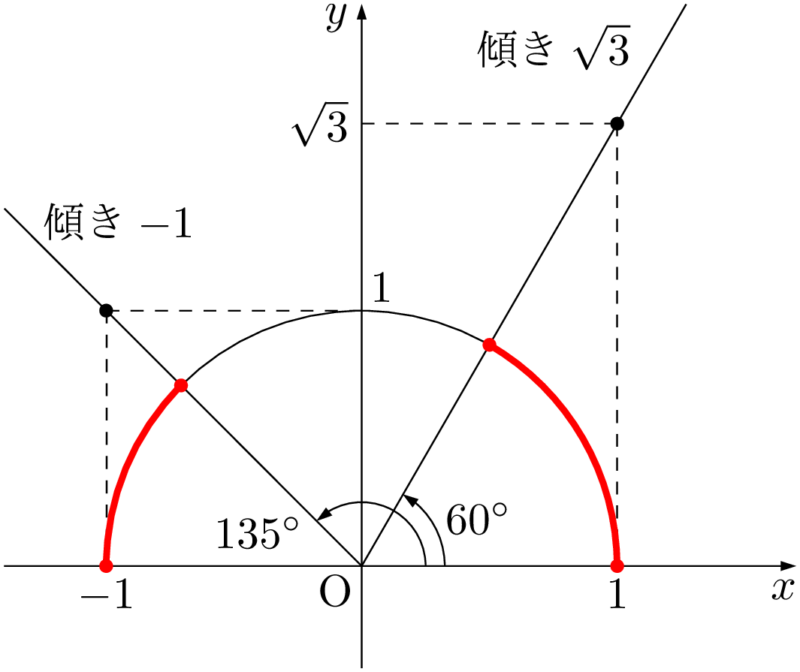
$0\Deg\leqq\theta\leqq180\Deg$ より,$0\Deg\leqq\theta\leqq60\Deg,~135\Deg\leqq\theta\leqq180\Deg$
$\tan\theta=t$ とおくと $t$ の2次不等式になるね。ここでは文字を置き換えずに進めていこう。与えられた不等式より
\begin{align*} &(\tan\theta+1)(\tan\theta-\sqrt{3})\leqq0 \\[4pt] &-1\leqq\tan\theta\leqq\sqrt{3} \end{align*}
2点 $(1,~\sqrt{3}),~(-1,~1)$ を利用して2直線 $y=\sqrt{3}x,~y=-x$ を描こう。
$0\Deg\leqq\theta\leqq180\Deg$ より,$0\Deg\leqq\theta\leqq60\Deg,~135\Deg\leqq\theta\leqq180\Deg$

ヒロ
第1象限については傾きの大小関係を勘違いすることはほとんどないだろう。

ヒロ
しかし第2象限については傾きの大小関係を勘違いすることがあるので注意しよう。





















