ここでは自然数の正の約数の個数とその総和について説明します。
公式の意味も分からず,その公式を覚えているだけでは,問題が少し難しくなるとさっぱり分からなくなってしまいます。
複雑な問題にも対応できるように,公式の意味をしっかりと理解しましょう。
Contents
1種類の素因数の積からなる数の約数の個数とその約数の総和

ヒロ
まずは簡単な問題から理解していこう。
問題16の正の約数の個数とその約数の総和を求めよ。

ヒロ
まずは約数の個数から考えよう。
【正の約数の個数を求める】
16を素因数分解すると,$16=2^4$ となる。
素因数が2の1種類のため,2の個数を決めることで約数が1つ決まる。
例えば,2を2個取ると決めると,$2^2=4$ となり,16の約数の1つになる。
また,2を1個も取らないと決めたときは1を表す($2^0=1$)。
16は素因数2を4つ含むから,2の取り方は取らない場合を含めて全部で5通りあるから,求める正の約数の個数は5個である。
16を素因数分解すると,$16=2^4$ となる。
素因数が2の1種類のため,2の個数を決めることで約数が1つ決まる。
例えば,2を2個取ると決めると,$2^2=4$ となり,16の約数の1つになる。
また,2を1個も取らないと決めたときは1を表す($2^0=1$)。
16は素因数2を4つ含むから,2の取り方は取らない場合を含めて全部で5通りあるから,求める正の約数の個数は5個である。

ヒロ
次に約数の総和を考えよう。
【約数の総和を求める】
約数の和は
約数の和は
\begin{align*}
&1+2+2^2+2^3+2^4+2^5 \\[4pt]
&=1+2+4+8+16 \\[4pt]
&=31
\end{align*}
※等比数列の和の計算を考えて&1+2+2^2+2^3+2^4+2^5 \\[4pt]
&=1+2+4+8+16 \\[4pt]
&=31
\end{align*}
\begin{align*}
\dfrac{2^6-1}{2-1}=31
\end{align*}
と求めることもできる。\dfrac{2^6-1}{2-1}=31
\end{align*}
2種類以上の素因数の積からなる数の約数の個数とその約数の総和

ヒロ
次の問題を考えよう。
問題12の正の約数の個数とその約数の総和を求めよ。

ヒロ
まずは約数の個数を求めよう。
【12の正の約数の個数】
12を素因数分解すると
2の取り方のそれぞれに対して,3の取り方2通りがあるから,全部で $3\times2=6$ 通りの取り方がある。
12の正の約数を実際に書き出すと
12を素因数分解すると
\begin{align*}
12=2^2\times3
\end{align*}
となる。2と3の素因数の取る個数に着目すると,2は取らない場合から最大で2個取る場合までの3通りの取り方がある。素因数3については取らないか取るかの2通りの取り方がある。12=2^2\times3
\end{align*}
2の取り方のそれぞれに対して,3の取り方2通りがあるから,全部で $3\times2=6$ 通りの取り方がある。
12の正の約数を実際に書き出すと
\begin{align*}
1,~2,~3,~4~(=2^2),~6~(=2\Cdota3),~12~(=2^2\Cdota3)
\end{align*}
の6個ある。1,~2,~3,~4~(=2^2),~6~(=2\Cdota3),~12~(=2^2\Cdota3)
\end{align*}

ヒロ
次に約数の総和を求めよう。
【12の正の約数の総和】
12の正の約数が全部で6個あることが分かっているが,表を使って表すと次のようになる。
しかし単純に加えるという方法では,約数の個数が多くなったときに面倒になるから工夫することを考える。
数字が並んでいるだけの表も次のように「長さ」という意味を与えると違って見える。
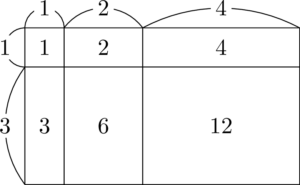
このようにすると,マスに書かれている数字は「面積」という意味をもつようになる。この図の6つの長方形の面積の和を求めるときに,どのように計算すれば良いかを考えよう。
縦の長さと横の長さを求めてその積を求めれば良いことが分かるだろう。つまり縦の長さは $1+3=4$,横の長さは $1+2+4=7$ であるから,6つのマスに書かれた数の和は
12の正の約数が全部で6個あることが分かっているが,表を使って表すと次のようになる。
\begin{align*}
\begin{array}{|c||c|c|c|}\hline
& 1 & 2 & 2^2 \\\hline
1 & 1 & 2 & 4 \\\hline
3 & 3 & 6 & 12 \\\hline
\end{array}\end{align*}
表の6つのマスの1, 2, 3, 4, 6, 12を加えれば約数の総和を求めることができる。\begin{array}{|c||c|c|c|}\hline
& 1 & 2 & 2^2 \\\hline
1 & 1 & 2 & 4 \\\hline
3 & 3 & 6 & 12 \\\hline
\end{array}\end{align*}
しかし単純に加えるという方法では,約数の個数が多くなったときに面倒になるから工夫することを考える。
数字が並んでいるだけの表も次のように「長さ」という意味を与えると違って見える。

このようにすると,マスに書かれている数字は「面積」という意味をもつようになる。この図の6つの長方形の面積の和を求めるときに,どのように計算すれば良いかを考えよう。
縦の長さと横の長さを求めてその積を求めれば良いことが分かるだろう。つまり縦の長さは $1+3=4$,横の長さは $1+2+4=7$ であるから,6つのマスに書かれた数の和は
\begin{align*}
(1+3)(1+2+4)=4\times7=28
\end{align*}
となる。これが3の約数の和と4の約数の和の積を表していることも分かる。(1+3)(1+2+4)=4\times7=28
\end{align*}
自然数の正の約数の個数とその約数の総和

ヒロ
それでは公式化しておこう。
約数の個数と総和ある自然数 $N$ が $N=a^p\Cdot b^q$ と素因数分解されるとき,$N$ の正の約数の個数とその総和は次のようになる。
\begin{align*}
&(約数の個数)=(p+1)(q+1) \\[4pt]
&(約数の総和)=(1+a+a^2+\cdots+a^p)(1+b+b^2+\cdots+b^q)
\end{align*}
&(約数の個数)=(p+1)(q+1) \\[4pt]
&(約数の総和)=(1+a+a^2+\cdots+a^p)(1+b+b^2+\cdots+b^q)
\end{align*}
【公式が成り立つ理由】
素因数 $a$ の取り方は取らない場合から $p$ 個取る場合までの $p+1$ 通りの取り方がある。また,素因数 $b$ の取り方は取らない場合から $q$ 個取る場合までの $q+1$ 通りの取り方がある。
$a$ の取り方それぞれに対して,$b$ の取り方が $q+1$ 通りあるのだから,全部で $(p+1)(q+1)$ 通りあることが分かる。つまり約数の個数が $(p+1)(q+1)$ 個あるということ。
また,約数の総和については,次の図のように長方形の面積を考える。
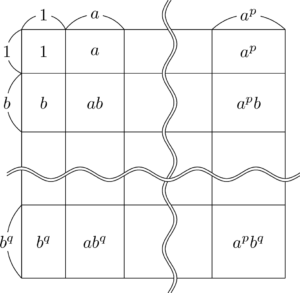
\begin{align*}
&(横の長さ)=1+a+\cdots+a^p \\[4pt]
&(縦の長さ)=1+b+\cdots+b^q
\end{align*}
であるから,長方形全体の面積は&(横の長さ)=1+a+\cdots+a^p \\[4pt]
&(縦の長さ)=1+b+\cdots+b^q
\end{align*}
\begin{align*}
(1+a+\cdots+a^p)(1+b+\cdots+b^q)
\end{align*}
であり,これが約数の総和でもある。(1+a+\cdots+a^p)(1+b+\cdots+b^q)
\end{align*}

ヒロ
$N$ を素因数分解したときに $a,~b,~c$ の3種類の素因数が現れたとしても同じようにして,約数の個数とその総和を求めることができる。
約数の個数と総和ある自然数 $N$ が $N=a^p\Cdot b^q\Cdot c^r$ と素因数分解されるとき,$N$ の正の約数の個数とその総和は次のようになる。
\begin{align*}
&(約数の個数)=(p+1)(q+1)(r+1) \\[4pt]
&(約数の総和)=(1+a+a^2+\cdots+a^p)(1+b+b^2+\cdots+b^q)(1+c+c^2+\cdots+c^r)
\end{align*}
&(約数の個数)=(p+1)(q+1)(r+1) \\[4pt]
&(約数の総和)=(1+a+a^2+\cdots+a^p)(1+b+b^2+\cdots+b^q)(1+c+c^2+\cdots+c^r)
\end{align*}
自然数の正の約数の個数とその約数の総和を求める問題

ヒロ
それでは実際に定期テストで出題された問題を解いてみよう。
問題360について
(1) 正の約数は全部でいくつあるか。
(2) 正の約数の総和を求めよ。
(1) 正の約数は全部でいくつあるか。
(2) 正の約数の総和を求めよ。

ヒロ
素因数分解を正確にすることができれば大丈夫だろう。
【解答】
(1) 360を素因数分解すると
(1) 360を素因数分解すると
\begin{align*}
360=2^3\times3^2\times5
\end{align*}
であるから,正の約数の個数は360=2^3\times3^2\times5
\end{align*}
\begin{align*}
4\times3\times2=24~個
\end{align*}
(2) 正の約数の総和は4\times3\times2=24~個
\end{align*}
\begin{align*}
&(1+2+2^2+2^3)(1+3+3^2)(1+5) \\[4pt]
&=15\times13\times6 \\[4pt]
&=1170
\end{align*}
&(1+2+2^2+2^3)(1+3+3^2)(1+5) \\[4pt]
&=15\times13\times6 \\[4pt]
&=1170
\end{align*}