ここでは無理関数の最小値について解説します。
無理関数の最小値を求める問題では,一般的な解法としては数学IIIの微分を用います。
しかし,ある特殊な形をした無理関数では,微分を利用することなく,その関数の最小値を求めることができます。
関数や式を見たときに考えること・思うことは,その関数や式によっても違いますし,人によっても異なります。ただ,「式の一つの見方」として知っておくことで,色々な問題に対応できるようになることもあります。知識を増やしていきましょう。
Contents
質問された問題

ヒロ先生,この問題って微分するしかないんですか?
問題
次の関数の最小値とそのときの $x$ の値を求めよ。
\begin{align*} y=\sqrt{x^2+1}+\sqrt{(x-3)^2+4} \end{align*}

ヒロ
解答は微分を利用して解いているんだよね?

そうです。やっぱり微分するしかないですか?

ヒロ
この問題の関数の形なら,実は微分をしなくても解けるよ。

その方法を教えて下さい!

ヒロ
それでは解いていこう!
数学IIIの微分を用いない解法

ヒロ
まず,つぎのような式の見方をできるようにしよう。
2点間の距離$\sqrt{(a-c)^2+(b-d)^2}$ は2点A $(a,b)$ とB $(c,d)$ の間の距離を表している。

ヒロ
今回の問題の $\sqrt{x^2+1}$ はどんな2点間の距離を表しているか考えよう。

2点 $(x,0)$ と $(0,1)$ の間の距離ですか?

ヒロ
いいね!では $\sqrt{(x-3)^2+4}$ の部分はどうかな?

同じように考えると,2点 $(x,0)$ と $(3,2)$ の間の距離ですか?

ヒロ
そうだね。
それでは,今考えた3点を座標平面にとってみよう。
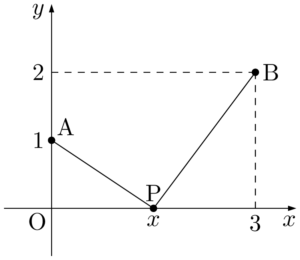

A$(0,1)$, B$(3,2)$, P$(x,0)$ として,点Pは $x$ 軸上に適当にとりました。

ヒロ
求める関数の最小値は,$\rm{AP+BP}$ の最小値ということだね。

2つの線分の長さの和の最小値を求める問題ですね!

ヒロ
そうだね!ここまできたら微分を利用しなくても解けることが分かるね。

やってみます!
$x$ 軸に関してAと対称な点をA$’$とすると,
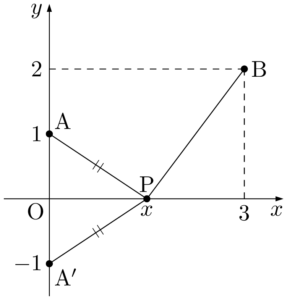
線分 $\rm{A’B}$ と $x$ 軸の交点をQとすると,点Pが点Qに一致するとき,$\rm{A’P+BP}$ が最小になる。
ここで,直線 $\rm{A’B}$ の方程式は $y=x-1$ だから,Q$(1,0)$ である。
また,$\rm{A’B}=\sqrt{3^2+3^2}=3\sqrt{2}$ であるから,
$x=1$ のとき,$y$ は最小値 $3\sqrt{2}$ をとる。
\begin{align*} \rm{AP+BP}=\rm{A’P+BP}\geqq\rm{A’B} \end{align*}

線分 $\rm{A’B}$ と $x$ 軸の交点をQとすると,点Pが点Qに一致するとき,$\rm{A’P+BP}$ が最小になる。
ここで,直線 $\rm{A’B}$ の方程式は $y=x-1$ だから,Q$(1,0)$ である。
また,$\rm{A’B}=\sqrt{3^2+3^2}=3\sqrt{2}$ であるから,
$x=1$ のとき,$y$ は最小値 $3\sqrt{2}$ をとる。

ヒロ
完璧だね!

合ってるんですね!良かったです!