Contents
微分係数とは

ヒロ
微分係数は次のように定義されている。
微分係数関数 $f(x)$ の $x=a$ における微分係数は
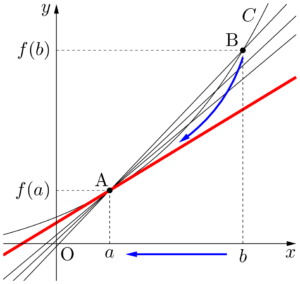
$f'(a)$ は直線ABの傾きの極限であるから,点Aにおける $C$ の接線の傾きが $f'(a)$ である。
\begin{align*}
f'(a)=\dlim{b\to a}\dfrac{f(b)-f(a)}{b-a}
\end{align*}
またはf'(a)=\dlim{b\to a}\dfrac{f(b)-f(a)}{b-a}
\end{align*}
\begin{align*}
f'(a)=\dlim{h\to0}\dfrac{f(a+h)-f(a)}{h}
\end{align*}
$y=f(x)$ のグラフを $C$ とし,$C$ 上に2点A$(a,~f(a))$,B$(b,~f(b))$ をとる。$b$ を $a$ に近づけるとき,点Bが $C$ 上を動きながら点Aに近づく。このとき,直線ABは点Aにおける $C$ の接線に近づく。f'(a)=\dlim{h\to0}\dfrac{f(a+h)-f(a)}{h}
\end{align*}

$f'(a)$ は直線ABの傾きの極限であるから,点Aにおける $C$ の接線の傾きが $f'(a)$ である。
2012年 高知工科大
2012年 高知工科大定数 $a$ を含む開区間で定義された関数 $y=f(x)$ の $x=a$ における微分係数 $f'(a)$ の定義を書け。また,その定義に従って,実数全体で定義された関数 $f(x)=x^2$ の $x=a$ における微分係数 $f'(a)$ を求めよ。
【解答と考え方】
定義を書く問題は,知っていれば正解できるから,覚えるべきことをしっかり覚えておこう。
$f'(a)=\dlim{h\to0}\dfrac{f(a+h)-f(a)}{h}$ において $h$ を限りなく0に近づけるとき,これがある値に限りなく近づくならば,その値を関数 $y=f(x)$ の $x=a$ における微分係数といい,$f'(a)$ で表す。すなわち
$f(x)=x^2$ のとき
定義を書く問題は,知っていれば正解できるから,覚えるべきことをしっかり覚えておこう。
$f'(a)=\dlim{h\to0}\dfrac{f(a+h)-f(a)}{h}$ において $h$ を限りなく0に近づけるとき,これがある値に限りなく近づくならば,その値を関数 $y=f(x)$ の $x=a$ における微分係数といい,$f'(a)$ で表す。すなわち
\begin{align*}
f'(a)=\dlim{h\to0}\dfrac{f(a+h)-f(a)}{h}
\end{align*}
である。f'(a)=\dlim{h\to0}\dfrac{f(a+h)-f(a)}{h}
\end{align*}
$f(x)=x^2$ のとき
\begin{align*}
f'(a)&=\dlim{h\to0}\dfrac{(a+h)^2-a^2}{h} \\[4pt]
&=\dlim{h\to0}(2a+h) \\[4pt]
&=2a
\end{align*}
f'(a)&=\dlim{h\to0}\dfrac{(a+h)^2-a^2}{h} \\[4pt]
&=\dlim{h\to0}(2a+h) \\[4pt]
&=2a
\end{align*}
2020年 東洋大
2020年 東洋大2次関数 $y=3x^2-2x+1$ の $x=1$ における微分係数は $\myhako$ である。
【解答と考え方】
$f(x)=3x^2-2x+1$ とおくと,微分係数の定義から
$f(x)=3x^2-2x+1$ とおくと,微分係数の定義から
\begin{align*}
f'(1)&=\dlim{h\to0}\dfrac{f(1+h)-f(1)}{h} \\[4pt]
&=\dlim{h\to0}\dfrac{3(1+h)^2-2(1+h)+1-2}{h} \\[4pt]
&=\dlim{h\to0}\dfrac{3h^2+4h}{h} \\[4pt]
&=\dlim{h\to0}(3h+4) \\[4pt]
&=4
\end{align*}
f'(1)&=\dlim{h\to0}\dfrac{f(1+h)-f(1)}{h} \\[4pt]
&=\dlim{h\to0}\dfrac{3(1+h)^2-2(1+h)+1-2}{h} \\[4pt]
&=\dlim{h\to0}\dfrac{3h^2+4h}{h} \\[4pt]
&=\dlim{h\to0}(3h+4) \\[4pt]
&=4
\end{align*}

ヒロ
答えを埋めれば良い問題のため,微分の計算方法を知っていれば,もっと簡単に求めることができる。

ヒロ
$f'(x)=6x-2$ となることが簡単に分かるから,$f'(1)=6-2=4$ となる。
2013年 関西学院大
2013年 関西学院大関数 $f(x)$ について $f(a)=p,~f'(a)=q$ が成り立つとき,
\begin{align*}
&\dlim{h\to0}\dfrac{f(a+2h)-f(a)}{h}=\myhako \\[4pt]
&\dlim{h\to0}\dfrac{\{f(a+h)\}^2-\{f(a)\}^2}{h}=\myhako
\end{align*}
である。&\dlim{h\to0}\dfrac{f(a+2h)-f(a)}{h}=\myhako \\[4pt]
&\dlim{h\to0}\dfrac{\{f(a+h)\}^2-\{f(a)\}^2}{h}=\myhako
\end{align*}
【解答と考え方】
今回の問題のように,いつも公式通りの形で出題されるとは限らない。定義通りの式でなくても,意味を理解することで解けるようになるだろう。
今回の問題のように,いつも公式通りの形で出題されるとは限らない。定義通りの式でなくても,意味を理解することで解けるようになるだろう。
\begin{align*}
&\dlim{h\to0}\dfrac{f(a+2h)-f(a)}{h} \\[4pt]
&=\dlim{h\to0}\dfrac{f(a+2h)-f(a)}{2h}\Cdota2 \\[4pt]
&=2f'(a)=2q
\end{align*}
2つ目の空欄も定義の+形が現れるように変形しよう。&\dlim{h\to0}\dfrac{f(a+2h)-f(a)}{h} \\[4pt]
&=\dlim{h\to0}\dfrac{f(a+2h)-f(a)}{2h}\Cdota2 \\[4pt]
&=2f'(a)=2q
\end{align*}
\begin{align*}
&\dlim{h\to0}\dfrac{\{f(a+h)\}^2-\{f(a)\}^2}{h} \\[4pt]
&=\dlim{h\to0}\dfrac{\{f(a+h)-f(a)\}\{f(a+2h)+f(a)\}}{h} \\[4pt]
&=\dlim{h\to0}\dfrac{f(a+h)-f(a)}{2h}\Cdota\{f(a+2h)+f(a)\} \\[4pt]
&=f'(a)\Cdota2f(a) \\[4pt]
&=2pq
\end{align*}
&\dlim{h\to0}\dfrac{\{f(a+h)\}^2-\{f(a)\}^2}{h} \\[4pt]
&=\dlim{h\to0}\dfrac{\{f(a+h)-f(a)\}\{f(a+2h)+f(a)\}}{h} \\[4pt]
&=\dlim{h\to0}\dfrac{f(a+h)-f(a)}{2h}\Cdota\{f(a+2h)+f(a)\} \\[4pt]
&=f'(a)\Cdota2f(a) \\[4pt]
&=2pq
\end{align*}


















