ここでは三角形の内接円と外接円について説明します。
三角形はその形状によらず,外接円・内接円を描くことができます。
三角形の3辺の長さが決まれば,その三角形の内接円の半径も決まるため,何らかの関係式を導くことができそうです。
意味を考えずに公式を覚えるのではなく,意味を考えて公式をいつでも導けるようにしておきましょう。
Contents
三角形の内接円

ヒロ
三角形の3辺に接する円を,その三角形の内接円という。

ヒロ
三角形の面積とその内接円の半径の間で成り立つ関係式を導こう。
【三角形の内接円】
次の図のような三角形ABCとその内接円について考える。
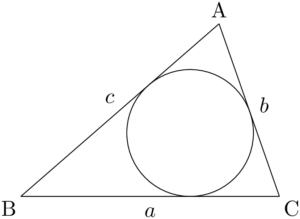
内接円の中心をIとし,半径を $r$ とする。
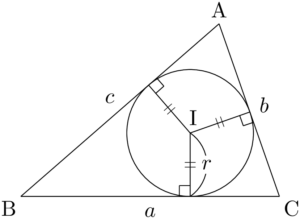
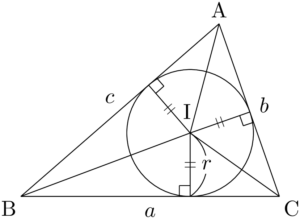
三角形の3つの頂点と内心Iを結んで3つの三角形に分割する。
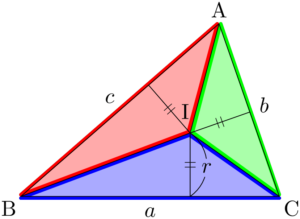
見やすいように色分けすると次のようになる。
$\sankaku{ABC}$ の面積を $S$ とすると
次の図のような三角形ABCとその内接円について考える。

内接円の中心をIとし,半径を $r$ とする。

三角形の3つの頂点と内心Iを結んで3つの三角形に分割する。

見やすいように色分けすると次のようになる。

$\sankaku{ABC}$ の面積を $S$ とすると
\begin{align*} S&=\textcolor{blue}{\sankaku{IBC}}+\textcolor{green}{\sankaku{ICA}}+\textcolor{red}{\sankaku{IAB}} \\[4pt] &=\dfrac{1}{2}ar+\dfrac{1}{2}br+\dfrac{1}{2}cr \\[4pt] &=\dfrac{1}{2}(a+b+c)r \end{align*}
と表される。よって,$\sankaku{ABC}$ の内接円の半径は\begin{align*}r=\dfrac{2S}{a+b+c}\end{align*}
で求めることができる。$\sankaku{ABC}$ の3辺の長さが分かっているから,余弦定理を利用して $\cos A$($\cos B$ や $\cos C$ でもよい) を求めて,さらに $\sin A$ を求めることで面積 $S$ を求めることができる。
ヒロ
外接円も考えることで色々な公式を導くことができる。
【三角形の内接円と外接円の半径】
$\sankaku{ABC}$ の面積 $S$ は
$\sankaku{ABC}$ の面積 $S$ は
\begin{align*}
S=\dfrac{1}{2}bc\sin A
\end{align*}
であるからS=\dfrac{1}{2}bc\sin A
\end{align*}
\begin{align*}
r&=\dfrac{bc\sin A}{a+b+c}
\end{align*}
また $\sankaku{ABC}$ の外接円の半径を $R$ とすると,正弦定理よりr&=\dfrac{bc\sin A}{a+b+c}
\end{align*}
\begin{align*}
\sin A=\dfrac{a}{2R}
\end{align*}
であるから\sin A=\dfrac{a}{2R}
\end{align*}
\begin{align*}
r&=\dfrac{bc}{a+b+c}\Cdota\dfrac{a}{2R} \\[4pt]
&=\dfrac{abc}{2R(a+b+c)}
\end{align*}
さらに別の表し方を考える。r&=\dfrac{bc}{a+b+c}\Cdota\dfrac{a}{2R} \\[4pt]
&=\dfrac{abc}{2R(a+b+c)}
\end{align*}
\begin{align*}
b=2R\sin B,~c=2R\sin C
\end{align*}
を利用するとb=2R\sin B,~c=2R\sin C
\end{align*}
\begin{align*}
r&=\dfrac{\sin A}{a+b+c}\Cdota2R\sin B\Cdota2R\sin C \\[4pt]
&=\dfrac{4R^2}{a+b+c}\sin A\sin B\sin C
\end{align*}
r&=\dfrac{\sin A}{a+b+c}\Cdota2R\sin B\Cdota2R\sin C \\[4pt]
&=\dfrac{4R^2}{a+b+c}\sin A\sin B\sin C
\end{align*}

ヒロ
これらの関係式を $S$ について解くことによって,$S$ を求める公式も得られる。

ヒロ
まとめて書くと次のようになる。
三角形の面積と内接円・外接円の関係$\sankaku{ABC}$ の面積を $S$,内接円の半径を $r$,外接円の半径を $R$ とすると

\begin{align*}
&r=\dfrac{2S}{a+b+c}=\dfrac{abc}{2R(a+b+c)}=\dfrac{4R^2}{a+b+c}\sin A\sin B\sin C \\[4pt]
&S=\dfrac{r}{2}(a+b+c)=\dfrac{abc}{4R}=2R^2\sin A\sin B\sin C
\end{align*}
が成り立つ。&r=\dfrac{2S}{a+b+c}=\dfrac{abc}{2R(a+b+c)}=\dfrac{4R^2}{a+b+c}\sin A\sin B\sin C \\[4pt]
&S=\dfrac{r}{2}(a+b+c)=\dfrac{abc}{4R}=2R^2\sin A\sin B\sin C
\end{align*}

三角形の内接円と外接円に関する問題
2019年 立命館大中心Oの円 $O$ に内接している $\sankaku{ABC}$ を考える。$\text{AB}=7$, $\text{BC}=8$, $\text{CA}=5$ のとき,$\text{OC}=\myhako$ となり,$\sankaku{ABC}$ の面積は $\myhako$ になる。また,$\sankaku{ABC}$ に内接する円 $Q$ の半径は $\myhako$ であり,円 $O$ の面積は,円 $Q$ の面積の $\myhako$ 倍になる。
【考え方と解答】
問題文に「内接」とあるから「円 $O$ は三角形の内接円だ」と安易に思ってはいけない。「何が何に内接しているか」が重要である。円が三角形に内接しているなら,その円は三角形の内接円であるが,三角形が円に内接しているなら,その円は三角形の外接円である。
このことを理解していないと始まらないので注意しよう。
この問題では,$\sankaku{ABC}$ が円 $O$ に内接しているから,円 $O$ は $\sankaku{ABC}$ の外接円である。したがって,OCの長さは外接円の半径である。余弦定理と正弦定理を利用して求めよう。
余弦定理より
したがって,正弦定理より
求める内接円の半径を $r$ とすると
問題文に「内接」とあるから「円 $O$ は三角形の内接円だ」と安易に思ってはいけない。「何が何に内接しているか」が重要である。円が三角形に内接しているなら,その円は三角形の内接円であるが,三角形が円に内接しているなら,その円は三角形の外接円である。
このことを理解していないと始まらないので注意しよう。
この問題では,$\sankaku{ABC}$ が円 $O$ に内接しているから,円 $O$ は $\sankaku{ABC}$ の外接円である。したがって,OCの長さは外接円の半径である。余弦定理と正弦定理を利用して求めよう。
余弦定理より
\begin{align*}
\cos C&=\dfrac{8^2+5^2-7^2}{2\Cdot8\Cdot5} \\[4pt]
&=\dfrac{40}{2\Cdot8\Cdot5}=\dfrac{1}{2}
\end{align*}
であるから $C=60\Deg$ であり,$\sin C=\dfrac{\sqrt{3}}{2}$ である。\cos C&=\dfrac{8^2+5^2-7^2}{2\Cdot8\Cdot5} \\[4pt]
&=\dfrac{40}{2\Cdot8\Cdot5}=\dfrac{1}{2}
\end{align*}
したがって,正弦定理より
\begin{align*}
\text{OC}&=\dfrac{\text{AB}}{2\sin C} \\[4pt]
&=\dfrac{7}{\sqrt{3}}=\dfrac{7\sqrt{3}}{3}
\end{align*}
$\sankaku{ABC}$ の面積を $S$ とすると\text{OC}&=\dfrac{\text{AB}}{2\sin C} \\[4pt]
&=\dfrac{7}{\sqrt{3}}=\dfrac{7\sqrt{3}}{3}
\end{align*}
\begin{align*}
S&=\dfrac{1}{2}\text{BC}\Cdota\text{CA}\sin C \\[4pt]
&=\dfrac{1}{2}\Cdota8\Cdota5\Cdota\dfrac{\sqrt{3}}{2} \\[4pt]
&=10\sqrt{3}
\end{align*}
次の $\sankaku{ABC}$ の内接円の半径は $\sankaku{ABC}$ の面積を利用して求めよう。S&=\dfrac{1}{2}\text{BC}\Cdota\text{CA}\sin C \\[4pt]
&=\dfrac{1}{2}\Cdota8\Cdota5\Cdota\dfrac{\sqrt{3}}{2} \\[4pt]
&=10\sqrt{3}
\end{align*}
求める内接円の半径を $r$ とすると
\begin{align*}
r&=\dfrac{2S}{\text{AB}+\text{BC}+\text{CA}} \\[4pt]
&=\dfrac{2\Cdot10\sqrt{3}}{7+8+5} \\[4pt]
&=\sqrt{3}
\end{align*}
すべての円は相似であるから,面積比は半径の2乗の比と等しくなる。したがってr&=\dfrac{2S}{\text{AB}+\text{BC}+\text{CA}} \\[4pt]
&=\dfrac{2\Cdot10\sqrt{3}}{7+8+5} \\[4pt]
&=\sqrt{3}
\end{align*}
\begin{align*}
\dfrac{円Oの面積}{円Qの面積}&=\dfrac{\text{OC}^2}{r^2} \\[4pt]
&=\dfrac{\left(\dfrac{7}{\sqrt{3}}\right)^2}{(\sqrt{3})^2} \\[4pt]
&=\dfrac{\dfrac{49}{3}}{3}=\dfrac{49}{9}
\end{align*}
\dfrac{円Oの面積}{円Qの面積}&=\dfrac{\text{OC}^2}{r^2} \\[4pt]
&=\dfrac{\left(\dfrac{7}{\sqrt{3}}\right)^2}{(\sqrt{3})^2} \\[4pt]
&=\dfrac{\dfrac{49}{3}}{3}=\dfrac{49}{9}
\end{align*}

ヒロ
ちなみに,この問題では「名古屋三角形」を知っていれば,$C=60\Deg$ であることは計算することなく一瞬で分かる。



















