Contents
2018年 東洋大
2018年 東洋大$0\leqq\theta<2\pi$ のとき,不等式 $2\sin^2\theta+5\cos\theta<-1$ の解は $\dfrac{\myhako}{\myhako}\pi<\theta<\dfrac{\myhako}{\myhako}\pi$ である。
【考え方と解答】
$\sin\theta,~\cos\theta$ が混在する方程式や不等式では,どちらか一方に統一しよう。今回は $\cos\theta$ に統一する。与えられた不等式より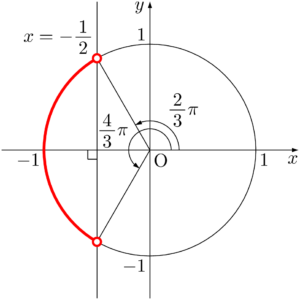
$0\leqq\theta<2\pi$ より,$\dfrac{2}{3}\pi<\theta<\dfrac{4}{3}\pi$
$\sin\theta,~\cos\theta$ が混在する方程式や不等式では,どちらか一方に統一しよう。今回は $\cos\theta$ に統一する。与えられた不等式より
\begin{align*} &2(1-\cos^2\theta)+5\cos\theta<-1 \\[4pt] &2\cos^2\theta-5\cos\theta-3>0 \\[4pt]
&(\cos\theta-3)(2\cos\theta+1)>0
\end{align*}
$\cos\theta-3<0$ であるから &(\cos\theta-3)(2\cos\theta+1)>0
\end{align*}
\begin{align*} &2\cos\theta+1<0 \\[4pt] &\cos\theta<-\dfrac{1}{2} \end{align*}

$0\leqq\theta<2\pi$ より,$\dfrac{2}{3}\pi<\theta<\dfrac{4}{3}\pi$
2019年 愛知学院大
2019年 愛知学院大$x$ の2次方程式 $4x^2+4(\cos\theta+1)x+(5\cos^2\theta+1)=0$(ただし $0\leqq\theta\leqq\pi$)について,次を求めなさい。
この方程式が異なる2つの実数解をもつときの $\theta$ の範囲は $\myhako$ となる。
この方程式が異なる2つの実数解をもつときの $\theta$ の範囲は $\myhako$ となる。
【考え方と解答】
与えられた2次方程式が異なる2つの実数解をもつのは,判別式を $D$ とすると,$D>0$ となるときであるから
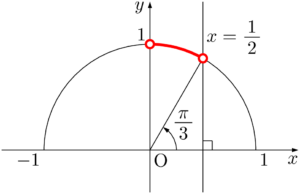
$0\leqq\theta\leqq\pi$ より,$\dfrac{\pi}{3}<\theta<\dfrac{\pi}{2}$
与えられた2次方程式が異なる2つの実数解をもつのは,判別式を $D$ とすると,$D>0$ となるときであるから
\begin{align*}
&\dfrac{D}{4}=4(\cos\theta+1)^2-4(5\cos^2\theta+1)>0 \\[4pt]
&(\cos\theta+1)^2-(5\cos^2\theta+1)>0 \\[4pt]
&-4\cos^2\theta+2\cos\theta>0 \\[4pt]
&\cos\theta(2\cos\theta-1)<0 \\[4pt] &0<\cos\theta<\dfrac{1}{2} \end{align*}
&\dfrac{D}{4}=4(\cos\theta+1)^2-4(5\cos^2\theta+1)>0 \\[4pt]
&(\cos\theta+1)^2-(5\cos^2\theta+1)>0 \\[4pt]
&-4\cos^2\theta+2\cos\theta>0 \\[4pt]
&\cos\theta(2\cos\theta-1)<0 \\[4pt] &0<\cos\theta<\dfrac{1}{2} \end{align*}

$0\leqq\theta\leqq\pi$ より,$\dfrac{\pi}{3}<\theta<\dfrac{\pi}{2}$


















