Contents
対数関数のグラフを描いてみよう

ヒロ
$y=\log_2x$ のグラフを描くことにする。
【$y=2^x$ のグラフ】
$x$ の値を色々変えて,対応する $y$ の値を求めると次のようになる。
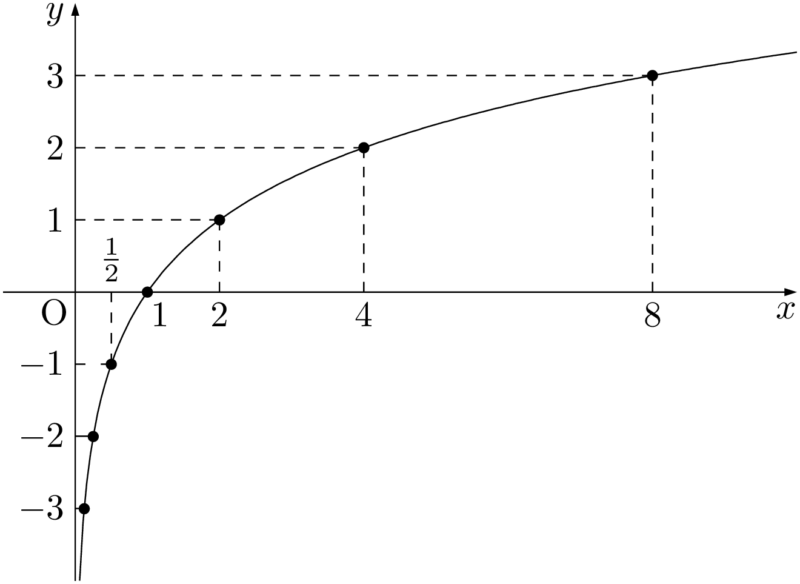
$x$ の値を色々変えて,対応する $y$ の値を求めると次のようになる。
\begin{align*}
\def\arraystretch{1.3}
\begin{array}{|c||c|c|c|c|c|c|c|}\hline
x & \dfrac{1}{8} & \dfrac{1}{4} & \dfrac{1}{2} & 1 & 2 & 4 & 8 \\\hline
y & -3 & -2 & -1 & 0 & 1 & 2 & 3 \\\hline
\end{array}
\end{align*}
座標平面上に点をとり,滑らかに結ぶと次のようになる。\def\arraystretch{1.3}
\begin{array}{|c||c|c|c|c|c|c|c|}\hline
x & \dfrac{1}{8} & \dfrac{1}{4} & \dfrac{1}{2} & 1 & 2 & 4 & 8 \\\hline
y & -3 & -2 & -1 & 0 & 1 & 2 & 3 \\\hline
\end{array}
\end{align*}


ヒロ
$y=\log_2x$ は $x$ の値が2倍になると $y$ の値が1増加する関数であり,緩やかに増加するのが分かるだろう。

ヒロ
$x$ の値が小さくなると,$y$ の値はどんどん小さくなるが,$x$ は常に正であるから,$y$ 軸にどんどん近づくが到達することはない。

ヒロ
つまり,$y$ 軸が漸近線になっている。

ヒロ
次に,$y=\log_{\frac{1}{2}}x$ のグラフを描く。
【$y=\log_{\frac{1}{2}}x$ のグラフ】
$x$ の値を色々変えて,対応する $y$ の値を求めると次のようになる。
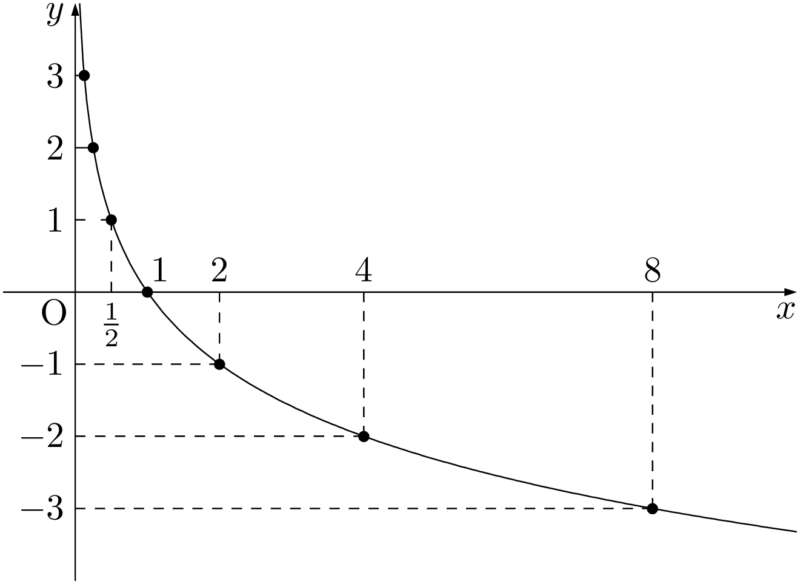
$x$ の値を色々変えて,対応する $y$ の値を求めると次のようになる。
\begin{align*}
\def\arraystretch{1.3}
\begin{array}{|c||c|c|c|c|c|c|c|}\hline
x & \dfrac{1}{8} & \dfrac{1}{4} & \dfrac{1}{2} & 1 & 2 & 4 & 8 \\\hline
y & 3 & 2 & 1 & 0 & -1 & -2 & -3 \\\hline
\end{array}
\end{align*}
座標平面上に点をとり,滑らかに結ぶと次のようになる。\def\arraystretch{1.3}
\begin{array}{|c||c|c|c|c|c|c|c|}\hline
x & \dfrac{1}{8} & \dfrac{1}{4} & \dfrac{1}{2} & 1 & 2 & 4 & 8 \\\hline
y & 3 & 2 & 1 & 0 & -1 & -2 & -3 \\\hline
\end{array}
\end{align*}


ヒロ
$y=\log_{\frac{1}{2}}x$ は $y=\log_2x$ のグラフと $x$ 軸に関して対称になっていることが分かる。

ヒロ
これは $\log_{\frac{1}{2}}x=\log_2x^{-1}=-\log_2x$ と変形できることを考えると,元の関数に $-1$ をかけたものになるから,グラフが $x$ 軸に関して対称になることも理解できる。
対数関数のグラフの特徴

ヒロ
対数関数 $y=\log_ax~(a>0,~a\neq1)$ のグラフの特徴をまとめておく。
$y=\log_ax~(a>1)$ のグラフの特徴
- グラフの概形
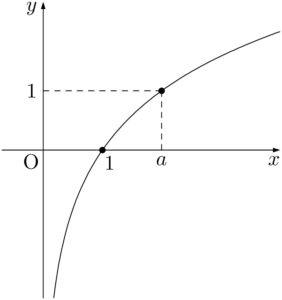
- $x$ の値が増加すると常に $y$ の値も増加する。
- 点 $(1,~0)$ を通る。
- $y$ 軸が漸近線である。
- $y=a^x$ のグラフと直線 $y=x$ に関して対称である。

ヒロ
次は $0<a<1$ のときの特徴。
$y=\log_ax~(0<a<1)$ のグラフの特徴
- グラフの概形
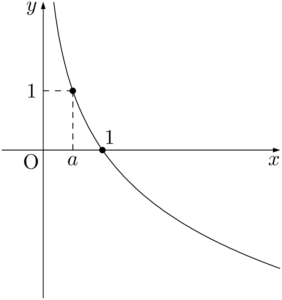
- $x$ の値が増加すると常に $y$ の値が減少する。
- 点 $(1,~0)$ を通る。
- $y$ 軸が漸近線である。
- $y=a^x$ のグラフと直線 $y=x$ に関して対称である。

ヒロ
下のアニメーションでは,底 $a$ の値に応じて,$y=\log_ax$ のグラフがどのように変化するかを確認することができる。



















