3次関数と直線で囲まれる2つの部分の面積が等しくなる問題について説明します。
3次関数のグラフが変曲点に関して点対称であることから,変曲点を通る直線と3次関数で囲まれる2つの部分の面積は等しくなります。
このことを知っていると,問題を解く際にも計算量を減らすことができ,計算を間違えることも少なくなるでしょう。
2020年 常葉大
2020年 常葉大$f(x)=x^3-5x^2+8x$ とし,$y=f(x)$ のグラフを $C$ とする。また,$a$ を実数の定数とし,直線 $y=ax$ を $l$ とする。$C$ と $l$ が $x>0$ の範囲で2個の共有点をもつような $a$ の値の範囲は
\begin{align*}
\dfrac{\myhako}{\myhako}<a<\myhako \end{align*}
である。このとき,$C$ と $l$ で囲まれる二つの範囲の面積が等しくなるのは,$a=\dfrac{\myhako}{\myhako}$ のときである。\dfrac{\myhako}{\myhako}<a<\myhako \end{align*}
【解答と考え方】
$C,~l$ の方程式から $y$ を消去すると
3次関数のグラフは変曲点に関して点対称であり,$C$ の変曲点の $x$ 座標は $\dfrac{5}{3}$ である。$y$ 座標は
$C,~l$ の方程式から $y$ を消去すると
\begin{align*} &x^3-5x^2+8x=ax \\[4pt] &x(x^2-5x+8-a)=0 \end{align*}
$C$ と $l$ が $x>0$ の範囲で2個の共有点をもつのは,$x^2-5x+8-a=0$ が異なる2つの正の解をもつときである。その2つの解を $\alpha,~\beta~(\alpha<\beta)$ とすると,求める条件は \begin{align*} 判別式~D>0~かつ~\alpha+\beta>0~かつ~\alpha\beta>0
\end{align*}
である。\end{align*}
\begin{align*}
\begin{cases}
D=25-4(8-a)>0 \\[4pt]
\alpha+\beta=5>0 \\[4pt]
\alpha\beta=8-a>0
\end{cases}
\end{align*}
これを解いて,$\dfrac{7}{4}<a<8$ 正確なグラフを描く必要はないが,一応描いておく。$f(x)=x^3-5x^2+8x$ のとき,\begin{cases}
D=25-4(8-a)>0 \\[4pt]
\alpha+\beta=5>0 \\[4pt]
\alpha\beta=8-a>0
\end{cases}
\end{align*}
\begin{align*} f'(x)&=3x^2-10x+8 \\[4pt] &=(x-2)(3x-4) \end{align*}
$f'(x)=0$ とすると,$x=2,~\dfrac{3}{4}$ よって,$f(x)$ の増減は次のようになる。\begin{align*} \begin{array}{|c||c|c|c|c|c|}\hline x & \cdots & -\dfrac{3}{4} & \cdots & 2 & \cdots \\\hline f'(x) & + & 0 & – & 0 & + \\\hline f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\\hline \end{array} \end{align*}
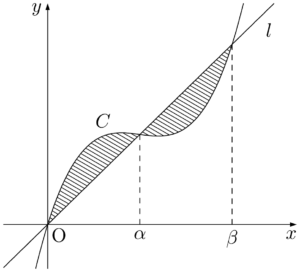
$C$ と $l$ で囲まれた2つの部分は次の図の斜線部分である。
3次関数のグラフは変曲点に関して点対称であり,$C$ の変曲点の $x$ 座標は $\dfrac{5}{3}$ である。$y$ 座標は
\begin{align*} f\left(\dfrac{5}{3}\right)&=\dfrac{125}{27}-\dfrac{125}{9}+\dfrac{40}{3} \\[4pt] &=\dfrac{125-375+360}{27} \\[4pt] &=\dfrac{110}{27} \end{align*}
したがって,2つの部分の面積が等しくなるのは,$l$ が点 $\left(\dfrac{5}{3},\dfrac{110}{27}\right)$ を通るときである。このとき \begin{align*} a&=\dfrac{\dfrac{110}{27}}{\dfrac{5}{3}}=\dfrac{22}{9} \end{align*}

ヒロ
3次関数のグラフが変曲点に関して点対称であることについては,次の記事で扱っている。

ヒロ
3次関数の対称性について知らない場合は,定積分の計算に頼ることになるだろう。

ヒロ
ただし,できれば工夫して計算量を減らすと良い。
【別解と考え方】
2つの部分の面積が等しいとき
2つの部分の面積が等しいとき
\begin{align*} \dint{0}{\alpha}\{f(x)-ax\}\;dx=\dint{\alpha}{\beta}\{ax-f(x)\}\;dx \end{align*}
が成り立つ。このまま計算するのは大変なので,簡単な形になるまで変形しよう。 \begin{align*} &\dint{0}{\alpha}\{f(x)-ax\}\;dx-\dint{\alpha}{\beta}\{ax-f(x)\}\;dx=0 \\[4pt] &\dint{0}{\alpha}\{f(x)-ax\}\;dx+\dint{\alpha}{\beta}\{f(x)-ax\}\;dx=0 \\[4pt] &\dint{0}{\beta}\{f(x)-ax\}\;dx=0 \end{align*}
ここまで変形することで $\alpha$ を使わなくても良くなる。 \begin{align*} &\dint{0}{\beta}\{f(x)-ax\}\;dx \\[4pt] &=\dint{0}{\beta}\{x^3-5x^2+(8-a)x\}\;dx \\[4pt] &=\Tint{\dfrac{1}{4}x^4-\dfrac{5}{3}x^3+\dfrac{8-a}{2}x^2}{0}{\beta} \\[4pt] &=\dfrac{1}{4}\beta^4-\dfrac{5}{3}\beta^3+\dfrac{8-a}{2}\beta^2 \end{align*}
であり,$\beta>0$ であるから\begin{align*}
&\dfrac{1}{4}\beta^2-\dfrac{5}{3}\beta+\dfrac{8-a}{2}=0 \\[4pt]
&\dfrac{1}{2}\beta^2-\dfrac{5}{3}\beta+8-a=0\cdots\cdots①
\end{align*}
また,$C$ と $l$ は $x=\beta$ の点で交わっているから&\dfrac{1}{4}\beta^2-\dfrac{5}{3}\beta+\dfrac{8-a}{2}=0 \\[4pt]
&\dfrac{1}{2}\beta^2-\dfrac{5}{3}\beta+8-a=0\cdots\cdots①
\end{align*}
\begin{align*}
&\beta^3-5\beta^2+8\beta=a\beta \\[4pt]
&\beta^2-5\beta+8-a=0~\cdots\cdots②
\end{align*}
$②-①$ より&\beta^3-5\beta^2+8\beta=a\beta \\[4pt]
&\beta^2-5\beta+8-a=0~\cdots\cdots②
\end{align*}
\begin{align*}
&\dfrac{1}{2}\beta^2-\dfrac{10}{3}\beta=0 \\[4pt]
&\beta=\dfrac{10}{3}
\end{align*}
このとき,②より&\dfrac{1}{2}\beta^2-\dfrac{10}{3}\beta=0 \\[4pt]
&\beta=\dfrac{10}{3}
\end{align*}
\begin{align*}
a&=\dfrac{100}{9}-\dfrac{50}{3}+8 \\[4pt]
&=\dfrac{100-150+72}{9} \\[4pt]
&=\dfrac{22}{9}
\end{align*}
a&=\dfrac{100}{9}-\dfrac{50}{3}+8 \\[4pt]
&=\dfrac{100-150+72}{9} \\[4pt]
&=\dfrac{22}{9}
\end{align*}



















