ここでは異なるものを円形に並べる順列(円順列)の総数を求める方法や考え方について説明します。
円形に並べるときには,回転すると同じ並び方になるものはすべて同じ順列として扱うことに注意する必要があります。
「円順列の公式」というものがありますが,個人的には「結局公式は?」と聞く人を黙らせるものという認識です。
公式を知っているだけでは解けない問題は多くあるため,学校の定期テスト程度の問題なら通用しても,大学入試に出題される問題を解くことはできません。
しっかりした考え方を身に付けることで,大学入試に出題される複雑な問題にも対応することができます。
Contents
円形に並べるのは1列に並べるのと何が異なるのか?

まずは円形に並べる場合と1列に並べる場合の違いについて理解しよう。
例えばA, B, Cの3つの文字を円形に並べる方法は,次の2通りしかない。
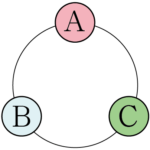
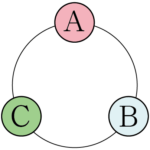
次の3つの並べ方は,異なる並べ方に見えるが,最初の並べ方を時計回りに $120\Deg$ ずつ回転させただけである。

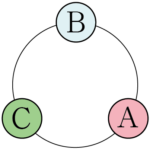
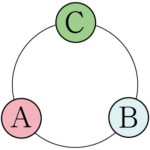
このように,1列に並べる場合と異なり,円順列では回転させると同じ並べ方になるものが存在する。円順列では,回転させると同じ並べ方になるものは,それぞれを区別せずに1つの並べ方と見る。
円順列の総数の求め方

円順列の総数を求める方法として,主に2つの方法がある。
- 回転しないように固定する
- 回転して重複するものを除く

1つずつ説明していこう。
回転しないように固定する

1列に並べる場合と異なり,回転すると同じ並べ方が発生してしまうため,そもそも回転できないように,1つのものを固定することで順列の総数を数えやすくなる。

A, B, Cの3文字を円形に並べる方法を例として考えよう。
まず,回転しないように1つの文字を固定する。固定する文字はどれでも良い。このときに,固定する文字はA, B, Cの3文字あるから「まず3通り」などとするのはダメ。Aに着目した場合「Aはどこかにあるはずだから,それを上に持ってきても良いよね」という感じで固定しているだけということを意識しよう。
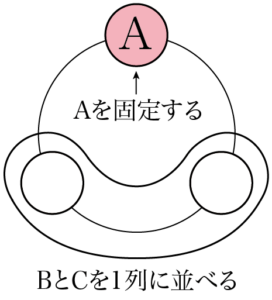
Aを上にもってきて固定すると,残りBとCを並べることになり,これは円形ではないから $2!=2$ 通りの並べ方がある。
よって,3文字A, B, Cを円形に並べる方法は2通りあることが分かる。
回転して重複するものを除く

1列に並べる場合を考えると,$3!=6$ 通りある。ただし,この中には回転すると同じ並べ方も含まれているので,それらを除くことを考える。

しかし,具体的な並べ方を考えて「これらが重複しているから除く」などとするのでは,計算で求めることができなくなる。

3文字を並べるという簡単な問題であっても,より複雑な問題に対応できるように一般化できる考え方を身に付けよう。
3文字を円形に並べる1つの並べ方に対して,回転させて同じ並べ方になるものが何通りあるかを考える。1つの並べ方を回転させていくと,3通りの並べ方ができることが分かる。



回転させても別の並べ方とするなら3通りあるが,この3通りを1通りと見るのが円順列の考え方となるため「3で割る」ことで計算で求めることができるようになる。
つまり,3文字を1列に並べる方法が $3!$ 通りあるから,これを3で割って
\dfrac{3!}{3}=2~通り
\end{align*}

2つの考え方があるが,どちらかと言えば,回転しないように1つのものを固定する考え方の方が楽だと思う。

一応,公式を載せておくと次のようになる。
定期テストで出題された問題

それでは実際に定期テストで出題された問題を解いてみよう。
回転しないように,まず1人を固定しよう。1人を固定することで残りの4人を並べる方法は,曲がっているけど1列に並べる方法に等しくなる。
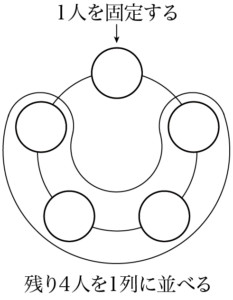
したがって,求める場合の数は
4!=24~通り
\end{align*}
定期テストで出題された問題2

次も定期テストで出題された問題。
(1) 円形に並ぶ。
(2) 女子3人が隣り合うように,円形に並ぶ。
(3) 女子が隣り合わないように,円形に並ぶ。

円形に並ぶことに注意して考えていこう。
1人を固定して考えると,求める場合の数は残り7人を1列に並べる方法の総数に等しいから
7!=5040~通り
\end{align*}

「隣り合う」に注意して考えよう。
女子3人が隣り合うから1つのカタマリXにして考えよう。次の手順で条件を満たすように円形に並べることができる。
① Xと男子5人の計6人を円形に並べる。
② Xの中の女子3人を1列に並べる。
①の方法は1人を固定(例えばXを固定)して残り5人を並べるから $5!$ 通り。②の方法は $3!$ 通りある。よって,求める場合の数は
5!\times3!&=120\times6 \\[4pt]
&=720~通り
\end{align*}

「隣り合わない」に注意して考えよう。
次の手順で条件を満たすように円形に並べることができる。
① (隣り合っても良い)男子5人を円形に並べる。
② 円形に並べた男子5人の間5か所のうち,3か所に女子3人を並べる。
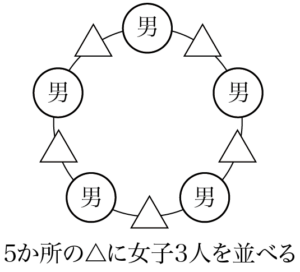
①の方法は $4!$ 通り。②の方法は1人ずつ並べる場所を考えて $5\Cdot4\Cdot3$ 通りある。よって,求める場合の数は
4!\times5\Cdota4\Cdota3&=24\times60 \\[4pt]
&=1440~通り
\end{align*}