Contents
相加・相乗平均の関係を利用して最小値を求める問題【星薬科大】
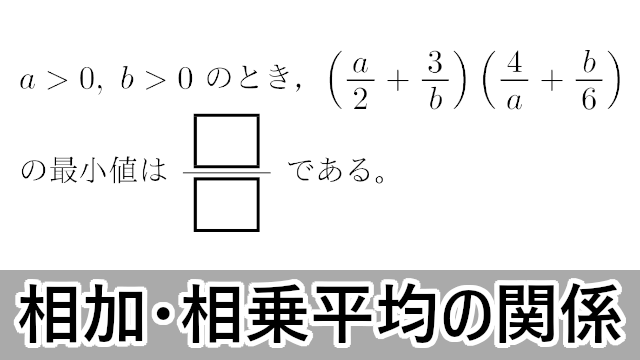
2019年 星薬科大$a>0,~b>0$ のとき,$\left(\dfrac{a}{2}+\dfrac{3}{b}\right)\left(\dfrac{4}{a}+\dfrac{b}{6}\right)$ の最小値は $\dfrac{\myhako}{\myhako}$ である。

ヒロ
分数式の最小値を求める問題では,相加・相乗平均の関係を利用することを検討してみよう。
【考え方と解答】
よって,求める最小値は $\dfrac{9}{2}$ である。
\begin{align*}
(与式)&=\dfrac{ab}{12}+\dfrac{12}{ab}+\dfrac{5}{2}
\end{align*}
$a,~b$ が正であるから,相加・相乗平均の関係より(与式)&=\dfrac{ab}{12}+\dfrac{12}{ab}+\dfrac{5}{2}
\end{align*}
\begin{align*}
&\dfrac{ab}{12}+\dfrac{12}{ab}\geqq2\sqrt{\dfrac{ab}{12}\Cdota\dfrac{12}{ab}}=2 \\[4pt]
&\dfrac{ab}{12}+\dfrac{12}{ab}+\dfrac{5}{2}\geqq2+\dfrac{5}{2}=\dfrac{9}{2}
\end{align*}
ここで,等号が成り立つのは $\dfrac{ab}{12}=\dfrac{12}{ab}=1$ すなわち $ab=12$ のときである。&\dfrac{ab}{12}+\dfrac{12}{ab}\geqq2\sqrt{\dfrac{ab}{12}\Cdota\dfrac{12}{ab}}=2 \\[4pt]
&\dfrac{ab}{12}+\dfrac{12}{ab}+\dfrac{5}{2}\geqq2+\dfrac{5}{2}=\dfrac{9}{2}
\end{align*}
よって,求める最小値は $\dfrac{9}{2}$ である。
相加・相乗平均の関係を利用して最小値を求めるときの注意点

ヒロ
最初の問題で,与式を展開せずに同じようにすると,解答は次のようなどこかおかしいものになる。
$a>0,~b>0$ のとき,$\left(\dfrac{a}{2}+\dfrac{3}{b}\right)\left(\dfrac{4}{a}+\dfrac{b}{6}\right)$ の最小値は $\dfrac{\myhako}{\myhako}$ である。
【何かがおかしい解答?】
$a,~b$ が正であるから,相加・相乗平均の関係より
\begin{align*}
\dfrac{a}{2}+\dfrac{3}{b}\geqq2\sqrt{\dfrac{3a}{2b}}~\cdots\cdots① \\[4pt]
\dfrac{4}{a}+\dfrac{b}{6}\geqq2\sqrt{\dfrac{2b}{3a}}~\cdots\cdots②
\end{align*}
①,②の辺々をかけて\dfrac{a}{2}+\dfrac{3}{b}\geqq2\sqrt{\dfrac{3a}{2b}}~\cdots\cdots① \\[4pt]
\dfrac{4}{a}+\dfrac{b}{6}\geqq2\sqrt{\dfrac{2b}{3a}}~\cdots\cdots②
\end{align*}
\begin{align*}
\left(\dfrac{a}{2}+\dfrac{3}{b}\right)\left(\dfrac{4}{a}+\dfrac{b}{6}\right)\geqq4~\cdots\cdots③
\end{align*}
\left(\dfrac{a}{2}+\dfrac{3}{b}\right)\left(\dfrac{4}{a}+\dfrac{b}{6}\right)\geqq4~\cdots\cdots③
\end{align*}

ヒロ
③を見ると,最小値は4だと思ってしまう。

ヒロ
しかも,どこも間違えているようには思えず,何が悪いのか分からなくなる。

ヒロ
また「解き方によって解答が異なる」という訳の分からないことになってしまう。
【何がおかしいのか?】
等号が成立するときに着目しよう。③の等号が成り立つのは,①と②の等号が同時に成り立つときである。
①の等号が成り立つのは $\dfrac{a}{2}=\dfrac{3}{b}$ すなわち $ab=6$ のときである。また,②の等号が成り立つのは $\dfrac{4}{a}=\dfrac{b}{6}$ すなわち $ab=24$ のときである。
つまり,①と②の等号が同時に成り立つことはないから,③の等号が成り立つこともない。
$\left(\dfrac{a}{2}+\dfrac{3}{b}\right)\left(\dfrac{4}{a}+\dfrac{b}{6}\right)$ は4以上の値をとると言えるが,実際には4になることはないということ。したがって,$\left(\dfrac{a}{2}+\dfrac{3}{b}\right)\left(\dfrac{4}{a}+\dfrac{b}{6}\right)$ の最小値が4であるとは言えない。

ヒロ
ということで,相加・相乗平均の関係を利用して,最小値や最大値を求めるときは「等号が成り立つときが存在するかどうか」に注意するようにしよう。

ヒロ
また一般的に,「積が一定」のときは,相加・相乗平均の関係を利用することで最小値を求められる。
相加・相乗平均の関係を利用して最大値を求める問題【慶應義塾大】
2020年 慶應義塾大正の実数 $x$ と $y$ が $9x^2+16y^2=144$ を満たしているとき,$xy$ の最大値は $\myhako$ である。
【考え方と解答】
今回,与えられている条件は「和が一定」である。この場合は,相加・相乗平均の関係をうまく利用することで,$xy$ の最大値を求めることができる。
$x$ と $y$ が正であるから,相加・相乗平均の関係より
よって,求める $xy$ の最大値は6である。
今回,与えられている条件は「和が一定」である。この場合は,相加・相乗平均の関係をうまく利用することで,$xy$ の最大値を求めることができる。
$x$ と $y$ が正であるから,相加・相乗平均の関係より
\begin{align*}
&\dfrac{9x^2+16y^2}{2}\geqq\sqrt{9x^2\Cdota16y^2} \\[4pt]
&\dfrac{144}{2}\geqq\abs{12xy} \\[4pt]
&xy\leqq6
\end{align*}
等号が成り立つのは,$9x^2=16y^2=72$ すなわち $x=2\sqrt{2},~y=\dfrac{3\sqrt{2}}{2}$ のときである。&\dfrac{9x^2+16y^2}{2}\geqq\sqrt{9x^2\Cdota16y^2} \\[4pt]
&\dfrac{144}{2}\geqq\abs{12xy} \\[4pt]
&xy\leqq6
\end{align*}
よって,求める $xy$ の最大値は6である。

ヒロ
分数関数の最大値や最小値を求める問題において,相加・相乗平均の関係を利用することが多いが,等号成立条件を常に確かめるようにしよう。