入試問題を扱って,3次関数の最大値と最小値に関する文章題を解説します。
文章題では,正しく立式することが重要です。
最大値や最小値を求めるものが2次関数であれば,平方完成して軸の位置に注意して最大値・最小値を求めることができます。
3次関数の場合は,微分して増減表を書くことで最大値・最小値を求めることができます。
「文章題」だからといってすぐに諦めるのではなく,ゆっくりで良いので一つずつ考えて解いていきましょう。
Contents
円柱の体積の最大値
2021年 金城学院大直円柱の体積を $y$,底面の円の半径を $x$ とする。表面積が $24\pi$ で一定のとき,次の問に答えなさい。
(1) $y=-\pi x^3+\myhako\pi x$ である。
(2) $x=\myhako$ のとき,$y$ は最大値 $\myhako\pi$ となる。
(1) $y=-\pi x^3+\myhako\pi x$ である。
(2) $x=\myhako$ のとき,$y$ は最大値 $\myhako\pi$ となる。
【(1)の解答と考え方】
直円柱の体積を求めるためには,底面積と高さを求める必要がある。まずは,この問題で与えられている底面の円の半径と表面積から円柱の高さを求めよう。
円柱の高さを $h$ とすると表面積が $24\pi$ であることから
直円柱の体積を求めるためには,底面積と高さを求める必要がある。まずは,この問題で与えられている底面の円の半径と表面積から円柱の高さを求めよう。
円柱の高さを $h$ とすると表面積が $24\pi$ であることから
\begin{align*}
&2\pi x^2+2\pi xh=24\pi \\[4pt]
&x^2+xh=12 \\[4pt]
&xh=-x^2+12
\end{align*}
したがって&2\pi x^2+2\pi xh=24\pi \\[4pt]
&x^2+xh=12 \\[4pt]
&xh=-x^2+12
\end{align*}
\begin{align*}
y&=\pi x^2h=\pi x\Cdot xh \\[4pt]
&=\pi x(-x^2+12) \\[4pt]
&=-\pi x^3+12\pi x
\end{align*}
y&=\pi x^2h=\pi x\Cdot xh \\[4pt]
&=\pi x(-x^2+12) \\[4pt]
&=-\pi x^3+12\pi x
\end{align*}
(2) $x=\myhako$ のとき,$y$ は最大値 $\myhako\pi$ となる。
【(2)の解答と考え方】
$x>0,~h>0$ であるから
$x>0,~h>0$ であるから
\begin{align*}
&-x^2+12>0 \\[4pt]
&0<x<2\sqrt{3} \end{align*}
$y=-\pi x^3+12\pi x$ より &-x^2+12>0 \\[4pt]
&0<x<2\sqrt{3} \end{align*}
\begin{align*} y’&=-3\pi x^2+12\pi \\[4pt] &=-3\pi(x^2-4) \\[4pt] &=-3\pi(x-2)(x+2) \end{align*}
$y’=0$ を解くと,$x=\pm2$ となるから,$y$ の増減は次のようになる。 \begin{align*} \begin{array}{|c||c|c|c|c|c|}\hline x & 0 & \cdots & 2 & \cdots & 2\sqrt{3} \\\hline y’ & & + & 0 & – & \\\hline y & & \nearrow & 極大 & \searrow & \\\hline \end{array} \end{align*}
よって,$x=2$ のとき $y$ は最大となる。最大値は \begin{align*} &-8\pi+24\pi=16\pi \end{align*}
正四角錐の体積の最大値
2021年 学習院大$0<t<\dfrac{5}{2}$ を満たす実数 $t$ に対して,1辺の長さが $2t$ の正方形を底面とし,4つの側面すべてが,底辺の長さが $2t$ で高さが $5-t$ の二等辺三角形である正四角錐の体積を $V$ とする。
(1) $V$ を求めよ。
(2) $t$ が $0<t<\dfrac{5}{2}$ の範囲を動くとき,$V$ の最大値と,最大値を与える $t$ の値を求めよ。
(1) $V$ を求めよ。
(2) $t$ が $0<t<\dfrac{5}{2}$ の範囲を動くとき,$V$ の最大値と,最大値を与える $t$ の値を求めよ。
【(1)の解答と考え方】
$V$ は正四角錐の体積であるから,底面積と高さを $t$ で表すことができれば $V$ を $t$ で表すことができる。底面は1辺の長さが $2t$ であるから,底面積は $4t^2$ となる。
次に高さを求める。問題文にある「高さ」は側面の三角形の高さであって,正四角錐の高さではない。勘違いしないようにしよう。
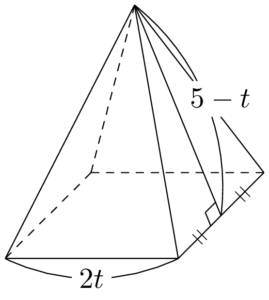
正四角錐を頂点と底面の各辺の中点を通る平面で切ったときの断面(灰色で塗った面)を考える。
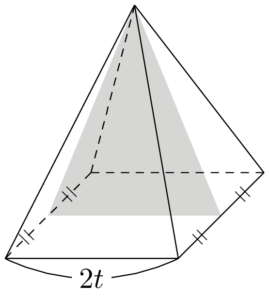
正四角錐の高さを $h$ とすると,断面は次のようになる。
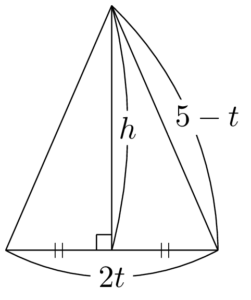
三平方の定理より
$V$ は正四角錐の体積であるから,底面積と高さを $t$ で表すことができれば $V$ を $t$ で表すことができる。底面は1辺の長さが $2t$ であるから,底面積は $4t^2$ となる。
次に高さを求める。問題文にある「高さ」は側面の三角形の高さであって,正四角錐の高さではない。勘違いしないようにしよう。

正四角錐を頂点と底面の各辺の中点を通る平面で切ったときの断面(灰色で塗った面)を考える。

正四角錐の高さを $h$ とすると,断面は次のようになる。

三平方の定理より
\begin{align*} h&=\sqrt{(5-t)^2-t^2} \\[4pt] &=\sqrt{25-10t} \end{align*}
したがって, \begin{align*} V&=\dfrac{1}{3}\Cdot4t^2\Cdot h \\[4pt] &=\dfrac{4}{3}t^2\sqrt{-10t+25} \end{align*}
(2) $t$ が $0<t<\dfrac{5}{2}$ の範囲を動くとき,$V$ の最大値と,最大値を与える $t$ の値を求めよ。
【(2)の解答と考え方】
「$V$ の最大値を求めよ」と言われても,根号を含む式の微分を知らなければ微分できないから,こんなのどうするんだ?となるかもしれない。根号の外の $t^2$ がなければ,また事情が異なる。この場合,根号の中にだけ $t$ があるから,根号内が最大になるときに $V$ も最大となる。このことから,根号の外にある $t^2$ を根号内にもっていくことで同じ考え方で $V$ の最大値を求めることができる。(1)の結果より
「$V$ の最大値を求めよ」と言われても,根号を含む式の微分を知らなければ微分できないから,こんなのどうするんだ?となるかもしれない。根号の外の $t^2$ がなければ,また事情が異なる。この場合,根号の中にだけ $t$ があるから,根号内が最大になるときに $V$ も最大となる。このことから,根号の外にある $t^2$ を根号内にもっていくことで同じ考え方で $V$ の最大値を求めることができる。(1)の結果より
\begin{align*} V&=\dfrac{4}{3}\sqrt{-10t^5+25t^4} \end{align*}
ここで $f(t)=-10t^5+25t^4$ とおく。 \begin{align*} f'(t)&=-50t^4+100t^3 \\[4pt] &=-50t^3(t-2) \end{align*}
$f'(t)=0$とすると,$t=0,2$ となるから,$0<t<\dfrac{5}{2}$ における $f(t)$ の増減は次のようになる。\begin{align*} \begin{array}{|c||c|c|c|c|c|}\hline t & 0 & \cdots & 2 & \cdots & \dfrac{5}{2} \\\hline f'(t) & & + & 0 & – & \\\hline f(t) & & \nearrow & 極大 & \searrow & \\\hline \end{array} \end{align*}
よって,$t=2$ のとき,$f(t)$ は最大になり,$V$ も最大になる。 $f(2)=4\sqrt{5}$ であるから,$V$ の最大値は $\dfrac{4}{3}f(2)=\dfrac{16}{3}\sqrt{5}$ であり,最大値を与える $t$ の値は $t=2$ である。

















