ここでは,三角関数の最大最小問題について説明します。
2次関数の最大最小問題に帰着させる問題では,定義域に注意しましょう。
2次関数の最大最小問題に関する知識があやふやな人は復習しておくと良いでしょう。
Contents
2020年 共立女子大
2020年 共立女子大$0\leqq x\leqq\pi$ のとき,$\sin^2x+\cos x-1$ の最大値と最小値および,それぞれの $x$ の値を求めなさい。
【考え方と解答】
$\cos x$ で統一して考えよう。$\cos x=t$ とおくと,与えられた式は $t$ の2次式で表せるが,その前に,変数変換をしたときには,まず定義域を確認しよう。
$\cos x=t$ とおくと,$0\leqq x\leqq\pi$ のとき,$-1\leqq t\leqq1$ である。与えられた式を $y$ とおくと
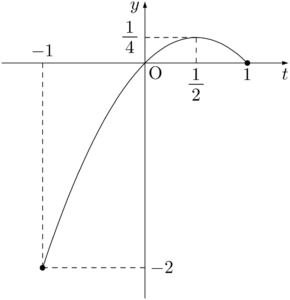
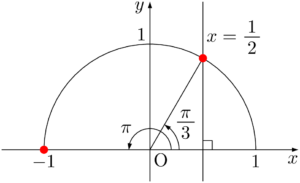
$t=\dfrac{1}{2}$ のとき,最大となり,$t=-1$ のとき,最小となる。
$x=\dfrac{\pi}{3}$ のとき,最大値 $\dfrac{1}{4}$ をとり,$x=\pi$ のとき,最小値 $-2$ をとる。
$\cos x$ で統一して考えよう。$\cos x=t$ とおくと,与えられた式は $t$ の2次式で表せるが,その前に,変数変換をしたときには,まず定義域を確認しよう。
$\cos x=t$ とおくと,$0\leqq x\leqq\pi$ のとき,$-1\leqq t\leqq1$ である。与えられた式を $y$ とおくと
\begin{align*}
y&=(1-t^2)+t-1 \\[4pt]
&=-\left(t-\dfrac{1}{2}\right)^2+\dfrac{1}{4}
\end{align*}
y&=(1-t^2)+t-1 \\[4pt]
&=-\left(t-\dfrac{1}{2}\right)^2+\dfrac{1}{4}
\end{align*}


$t=\dfrac{1}{2}$ のとき,最大となり,$t=-1$ のとき,最小となる。
$x=\dfrac{\pi}{3}$ のとき,最大値 $\dfrac{1}{4}$ をとり,$x=\pi$ のとき,最小値 $-2$ をとる。



















