ここでは,2次関数のグラフは動くような2次関数の最大値と最小値について説明します。
2次関数の最大値と最小値を求める問題では,軸と定義域の位置関係が重要です。
グラフが動くことによって,軸が定義域外になるかどうかに注目して考えられるようにしましょう。
グラフが動く2次関数の最大値と最小値を求める問題の考え方

ヒロ
軸と定義域の位置関係に応じて最大値をとる $x$ の値が変化することを知ろう。
【軸の位置で場合分け】
2次関数の $a\leqq x\leqq b$ における最大と最小は軸の位置によって場合分けをする。
グラフが下に凸のとき,それぞれの図において①~③で最大値をとり,❶~❸で最小値をとる。
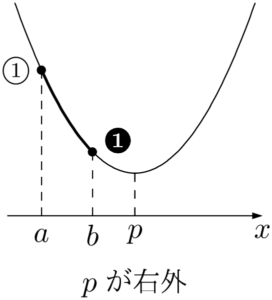
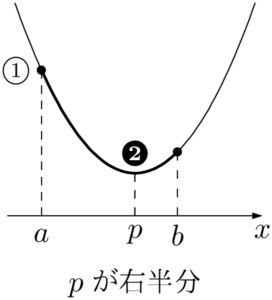
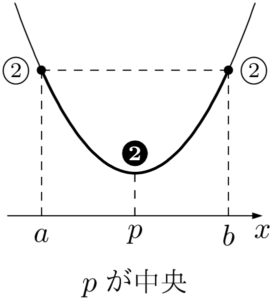
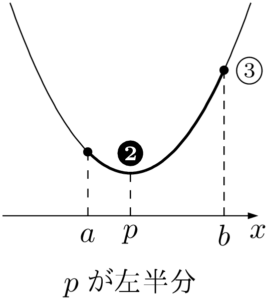
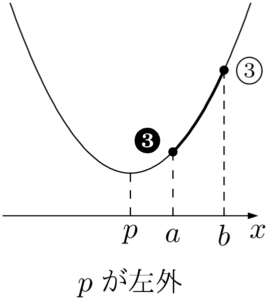
2次関数の $a\leqq x\leqq b$ における最大と最小は軸の位置によって場合分けをする。
グラフが下に凸のとき,それぞれの図において①~③で最大値をとり,❶~❸で最小値をとる。





2次関数の最大値と最小値を求める問題

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題関数 $y=-2x^2-4ax+3~(0\leqq x\leqq2)$ について,$a$ の値で場合分けして最大値と,そのときの $x$ の値を求めよ。

ヒロ
与えられた関数のグラフは上に凸の放物線になることと,軸と定義域の位置関係で場合分けしよう。
【考え方と解答】
与えられた関数のグラフは上に凸の放物線である。
$f(x)=-2x^2-4ax+3$ とおくと
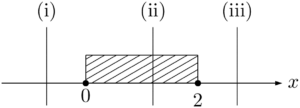
最大値は $x=0,~2,~-a$ のいずれかでとるから,それぞれのときの $y$ の値を先に求めておくと良い。
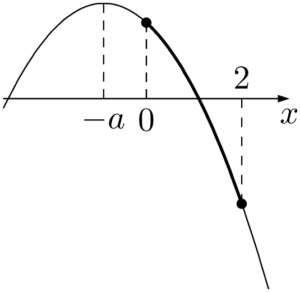
グラフより,最大値は $f(0)=3$
(ii) $0\leqq-a\leqq2$ すなわち $-2\leqq a\leqq0$ のとき
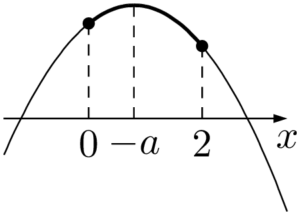
グラフより,最大値は $f(-a)=2a^2+3$
(iii) $2\leqq-a$ すなわち $a\leqq-2$ のとき
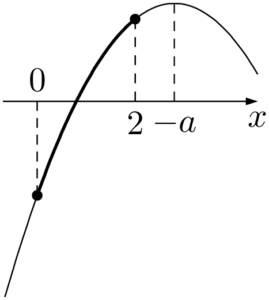
グラフより,最大値は $f(2)=-8a-5$
以上より,
$a\leqq-2$ のとき,$x=2$ で最大値 $-8a-5$
$-2\leqq a\leqq0$ のとき,$x=-a$ で最大値 $2a^2+3$
$0\leqq a$ のとき,$x=0$ で最大値 $3$
与えられた関数のグラフは上に凸の放物線である。
$f(x)=-2x^2-4ax+3$ とおくと
\begin{align*}
f(x)=-2(x+a)^2+2a^2+3
\end{align*}
軸の方程式が $x=-a$ で定義域が $0\leqq x\leqq2$ であるから,軸の位置で,次の(i)~(iii)の3つに場合分けをする。f(x)=-2(x+a)^2+2a^2+3
\end{align*}

最大値は $x=0,~2,~-a$ のいずれかでとるから,それぞれのときの $y$ の値を先に求めておくと良い。
\begin{align*}
&f(0)=3 \\[4pt]
&f(2)=-8a-5 \\[4pt]
&f(-a)=2a^2+3
\end{align*}
(i) $-a\leqq0$ すなわち $a\geqq0$ のとき&f(0)=3 \\[4pt]
&f(2)=-8a-5 \\[4pt]
&f(-a)=2a^2+3
\end{align*}

グラフより,最大値は $f(0)=3$
(ii) $0\leqq-a\leqq2$ すなわち $-2\leqq a\leqq0$ のとき

グラフより,最大値は $f(-a)=2a^2+3$
(iii) $2\leqq-a$ すなわち $a\leqq-2$ のとき

グラフより,最大値は $f(2)=-8a-5$
以上より,
$a\leqq-2$ のとき,$x=2$ で最大値 $-8a-5$
$-2\leqq a\leqq0$ のとき,$x=-a$ で最大値 $2a^2+3$
$0\leqq a$ のとき,$x=0$ で最大値 $3$
2次関数の最大値と最小値を求める問題

ヒロ
次の問題も実際に定期テストで出題された問題
問題2次関数 $y=x^2-2ax+3~(0\leqq x\leqq4)$ の最大値,最小値を求めよ。

ヒロ
さっきの問題のように,最大値と最小値の片方だけではなく,両方を求める問題だから,5つに場合分けをしよう。
【考え方と解答】
与えられた関数のグラフは下に凸の放物線である。
$f(x)=x^2-2ax+3$ とおくと
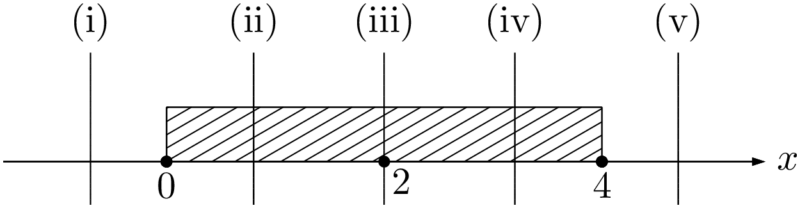
最大値と最小値は $x=0,~4,~a$ のいずれかでとるから,それぞれのときの $y$ の値を先に求めておくと良い。
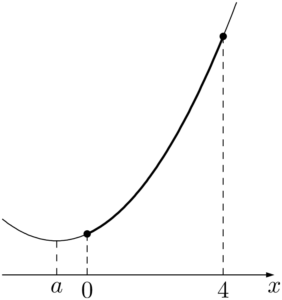
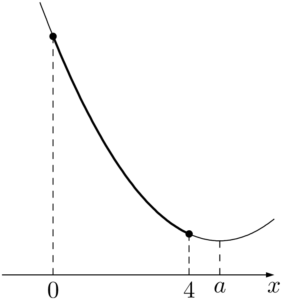
グラフより,$x=4$ で最大値 $-8a+19$ をとり,$x=0$ で最小値 $3$ をとる。
(ii) $0\leqq a<2$ のとき
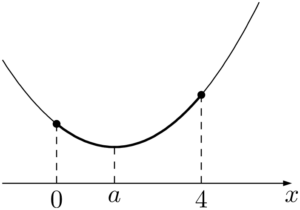
グラフより,$x=4$ で最大値 $-8a+19$ をとり,$x=a$ で最小値 $-a^2+3$ をとる。
(iii) $a=2$ のとき
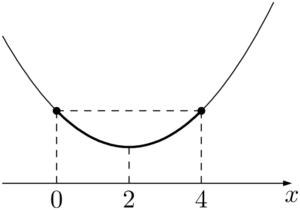
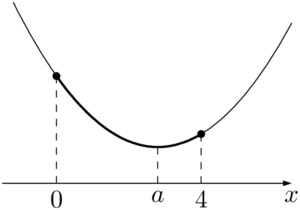
グラフより,$x=0,~4$ で最大値 $3$ をとり,$x=2$ で最小値 $-1$ をとる。(iv) $2<a\leqq4$ のとき
与えられた関数のグラフは下に凸の放物線である。
$f(x)=x^2-2ax+3$ とおくと
\begin{align*}
f(x)=(x-a)^2-a^2+3
\end{align*}
軸の方程式が $x=a$ で定義域が $0\leqq x\leqq4$ であるから,軸の位置で,次の(i)~(v)の5つに場合分けをする。f(x)=(x-a)^2-a^2+3
\end{align*}

最大値と最小値は $x=0,~4,~a$ のいずれかでとるから,それぞれのときの $y$ の値を先に求めておくと良い。
\begin{align*}
&f(0)=3 \\[4pt]
&f(4)=-8a+19 \\[4pt]
&f(a)=-a^2+3
\end{align*}
(i) $a<0$ のとき&f(0)=3 \\[4pt]
&f(4)=-8a+19 \\[4pt]
&f(a)=-a^2+3
\end{align*}

グラフより,$x=4$ で最大値 $-8a+19$ をとり,$x=0$ で最小値 $3$ をとる。
(ii) $0\leqq a<2$ のとき

グラフより,$x=4$ で最大値 $-8a+19$ をとり,$x=a$ で最小値 $-a^2+3$ をとる。
(iii) $a=2$ のとき

グラフより,$x=0,~4$ で最大値 $3$ をとり,$x=2$ で最小値 $-1$ をとる。(iv) $2<a\leqq4$ のとき

グラフより,$x=0$ で最大値 $3$ をとり,$x=a$ で最小値 $-a^2+3$ をとる。
(v) $4<a$ のとき

グラフより,$x=0$ で最大値 $3$ をとり,$x=4$ で最小値 $-8a+19$ をとる。


















