ここでは,2次関数の最大値と最小値について説明します。
1次関数のグラフのように,グラフが直線であれば,最大値と最小値を求めるのは簡単です。
しかし,2次関数のグラフは放物線であるため,端点以外に頂点に注意する必要があります。
したがって,2次関数の最大値・最小値を求めるときにはグラフを描いて考えるようにしましょう。
2次関数の最大値と最小値を求める問題

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題次の関数に最大値,最小値があれば,それを求めよ。またそのときの $x$ の値も書け。ただし,最大値,最小値がない場合は“なし”と答えよ。
\begin{align*} y=-x^2-2x+4~(-2<x\leqq1) \end{align*}

ヒロ
グラフを描くために平方完成しよう。
【考え方と解答】
\begin{align*}y=-x^2-2x+4~(-2<x\leqq1)\end{align*}
よって,グラフは次のようになる。
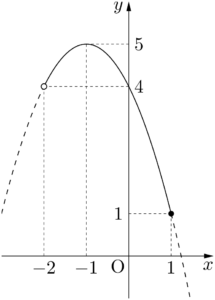
グラフより,最大値5($x=-1$ のとき),最小値1($x=1$ のとき)
2次関数の最大値と最小値に関する問題

ヒロ
次は最小値が与えられていて,関数を決定する問題。
問題関数 $y=-x^2+6x+c~(1\leqq x\leqq4)$ の最小値が $-2$ であるように,定数 $c$ の値を定めよ。また,そのときの最大値を求めよ。

ヒロ
グラフを描いて考えるために平方完成しよう。
【考え方と解答】
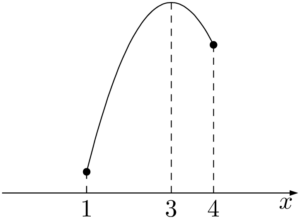
グラフより $x=1$ のときに最小となることが分かる。$y=f(x)$ とおくと,最小値が $-2$ のとき,$f(1)=-2$ が成り立つから,
\begin{align*}
y&=-x^2+6x+c \\[4pt]
&=-(x-3)^2+c+9
\end{align*}
軸と定義域の関係が分かれば良いので,次のように $y$ 軸を省略したグラフを描いて考える。y&=-x^2+6x+c \\[4pt]
&=-(x-3)^2+c+9
\end{align*}

グラフより $x=1$ のときに最小となることが分かる。$y=f(x)$ とおくと,最小値が $-2$ のとき,$f(1)=-2$ が成り立つから,
\begin{align*}
&-1+6+c=-2 \\[4pt]
&c=-7
\end{align*}
$x=3$ で最大となるから,このときの最大値は&-1+6+c=-2 \\[4pt]
&c=-7
\end{align*}
\begin{align*}
f(3)=-7+9=2
\end{align*}
f(3)=-7+9=2
\end{align*}

ヒロ
$y$ 軸を描かないグラフを描けるようにしよう。


















