ここでは,2次関数のグラフ(放物線)の平行移動について説明します。
$x^2$ の係数が等しい2次関数のグラフはすべて平行移動したものになっています。
ちなみに $x^2$ の係数が異なる2次関数のグラフはすべて相似になっています。
詳しくは次の記事で説明しています。
放物線の平行移動

ヒロ
放物線の平行移動について,次のことを覚えておこう。

ヒロ
放物線の平行移動を考えるときは頂点に着目しよう。
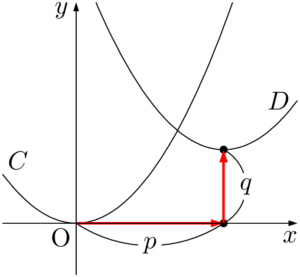
放物線の平行移動2次関数 $D:y=a(x-p)^2+q$ のグラフは,2次関数 $C:y=ax^2$ のグラフを $x$ 軸方向に $p$,$y$軸方向に $q$ だけ平行移動したものである。


ヒロ
平方完成して頂点の座標を求めれば,どのように平行移動するのかが分かるね。

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題放物線 $y=x^2-4x+4$ は,どのように平行移動すると放物線 $y=x^2+2x-1$ に重なるか。
【考え方と解答】
それぞれの放物線の式を平方完成して,頂点の座標を求めよう。
$y=x^2-4x+4$ より,$y=(x-2)^2$ となるから,頂点の座標は $(2,~0)$
$y=x^2+2x-1$ より,$y=(x+1)^2-2$ となるから,頂点の座標は $(-1,~-2)$
放物線 $y=x^2-4x+4$ を $x$ 軸方向に $p$,$y$ 軸方向に $q$ だけ平行移動すると放物線 $y=x^2+2x-1$ に重なるとすると,
それぞれの放物線の式を平方完成して,頂点の座標を求めよう。
$y=x^2-4x+4$ より,$y=(x-2)^2$ となるから,頂点の座標は $(2,~0)$
$y=x^2+2x-1$ より,$y=(x+1)^2-2$ となるから,頂点の座標は $(-1,~-2)$
放物線 $y=x^2-4x+4$ を $x$ 軸方向に $p$,$y$ 軸方向に $q$ だけ平行移動すると放物線 $y=x^2+2x-1$ に重なるとすると,
\begin{align*}
&2+p=-1,~0+q=-2 \\[4pt]
&p=-3,~q=-2
\end{align*}
よって,$x$ 軸方向に $-3$,$y$ 軸方向に $-2$ だけ平行移動する。&2+p=-1,~0+q=-2 \\[4pt]
&p=-3,~q=-2
\end{align*}
一般的な放物線のグラフの平行移動

ヒロ
上の問題をもとに,放物線のグラフの平行移動量から式を求める方法を考えよう。
【グラフの方程式と平行移動の関係】
放物線 $C:y=x^2-4x+4$ 上の任意の点を $\text{P}(x,~y)$ とする。
$C$ を $x$ 軸方向に $-3$,$y$ 軸方向に $-2$ だけ平行移動させたとき,点Pが点 $\text{Q}(X,~Y)$ に移ったとする。
上の結果から,$X,~Y$ は $Y=X^2+2X-1$ を満たすはずである。平行移動量を考えると
放物線 $C:y=x^2-4x+4$ 上の任意の点を $\text{P}(x,~y)$ とする。
$C$ を $x$ 軸方向に $-3$,$y$ 軸方向に $-2$ だけ平行移動させたとき,点Pが点 $\text{Q}(X,~Y)$ に移ったとする。
上の結果から,$X,~Y$ は $Y=X^2+2X-1$ を満たすはずである。平行移動量を考えると
\begin{align*}
&x-3=X,~y-2=Y \\[4pt]
&x=X+3,~y=Y+2
\end{align*}
となる。ここで,点 $\text{P}(x,~y)$ は $C$ 上にあるから&x-3=X,~y-2=Y \\[4pt]
&x=X+3,~y=Y+2
\end{align*}
\begin{align*}
&Y+2=(X+3)^2-4(X+3)+4 \\[4pt]
&Y=(X^2+6X+9)-4X-12+4-2 \\[4pt]
&Y=X^2+2X-1
\end{align*}
これは点 $\text{Q}(X,~Y)$ が放物線 $y=x^2+2x-1$ 上にあることを示している。&Y+2=(X+3)^2-4(X+3)+4 \\[4pt]
&Y=(X^2+6X+9)-4X-12+4-2 \\[4pt]
&Y=X^2+2X-1
\end{align*}
放物線の平行移動一般に,放物線 $C:y=ax^2+bx+c$ を $x$ 軸方向に $p$,$y$ 軸方向に $q$ だけ平行移動して得られるグラフを $D$ とすると,$D$ の方程式は,$C$ の $x$ を $x-p$,$y$ を $y-q$ として
\begin{align*}
&y-q=a(x-p)^2+b(x-p)+c \\[4pt]
&y=a(x-p)^2+b(x-p)+c+q
\end{align*}
と表される。&y-q=a(x-p)^2+b(x-p)+c \\[4pt]
&y=a(x-p)^2+b(x-p)+c+q
\end{align*}

ヒロ
点の座標の場合はそのまま平行移動量を加えることで,平行移動後の点の座標を求めることができる。

ヒロ
方程式になると「引く」から変な感じがするかもしれないが,$x$ 軸方向へ $p$ だけ平行移動する場合を考えると「$p$ だけ移動しても移動前の $y$ 座標と同じなのだから $p$ を引いて $x-p$ にしないといけない。」ということを理解できれば完璧。

ヒロ
これが理解できない人は「そういうもの」だと諦めよう(笑)

ヒロ
いずれ理解できる日が来るはず。

ヒロ
とりあえず問題を解いて慣れよう。
放物線のグラフの平行移動に関する問題
問題次の放物線を $x$ 軸方向に $1$,$y$ 軸方向に $-2$ だけ平行移動して得られる放物線の方程式を求めよ。
(1) $y=-3x^2$
(2) $y=2x^2+3$
(3) $y=x^2+3x-4$
(1) $y=-3x^2$
(2) $y=2x^2+3$
(3) $y=x^2+3x-4$

ヒロ
頂点の座標が簡単に分かる場合は,平行移動後の頂点の座標から方程式を求めた方が楽かもしれない。
【考え方と解答】
(1) 平行移動前の頂点は原点であるから,平行移動後の頂点の座標は $(1,~-2)$ である。よって,求める放物線の方程式は
(1) 平行移動前の頂点は原点であるから,平行移動後の頂点の座標は $(1,~-2)$ である。よって,求める放物線の方程式は
\begin{align*}
y&=-3(x-1)^2-2 \\[4pt]
&=-3x^2+6x-5
\end{align*}
(2) 平行移動前の頂点の座標は $(0,~3)$ であるから,平行移動後の頂点の座標は $(1,~1)$ である。よって,求める放物線の方程式はy&=-3(x-1)^2-2 \\[4pt]
&=-3x^2+6x-5
\end{align*}
\begin{align*}
y&=2(x-1)^2+1 \\[4pt]
&=2x^2-4x+3
\end{align*}
(3) $x$ を $x-1$,$y$ を $y+2$ にしてy&=2(x-1)^2+1 \\[4pt]
&=2x^2-4x+3
\end{align*}
\begin{align*}
&y+2=(x-1)^2+3(x-1)-4 \\[4pt]
&y=x^2+x-8
\end{align*}
&y+2=(x-1)^2+3(x-1)-4 \\[4pt]
&y=x^2+x-8
\end{align*}



















