ここでは平面ベクトルと三角形の外接円について解説します。
2つのベクトルの内積を求める問題では,求めたい内積を生み出す方法・考え方をいくつか知っておく必要があります。
問題で与えられている条件に応じて,求めたい内積が現れるような操作をできるようにしましょう。
2020年 芝浦工業大
2020年 芝浦工業大平面上に,$\sankaku{ABC}$ があり,その外接円の半径を1とし,外心をOとする。この $\sankaku{ABC}$ が $4\Vec{OA}+4\Vec{OB}+\Vec{OC}=\vec{0}$ 満たすとき,内積 $\Vec{OA}\Cdot\Vec{OB}$ の値は,$\myhako$ であり,$\sankaku{OAB}$ の面積は,$\sankaku{ABC}$ の面積の $\myhako$ 倍である。

ヒロ
2つのベクトルの内積が現れる基本的操作を知っておこう。
内積を作る$s\vec{a}+t\vec{b}+u\vec{c}=\vec{0}$ が成り立っているとき,$\vec{a}\Cdot\vec{b}$ を作る方法は主に2つある。
① $s\vec{a}+t\vec{b}=-u\vec{c}$ と変形して,両辺の大きさの2乗を考える。
② 両辺それぞれと $\vec{a}$ との内積を考える。
① $s\vec{a}+t\vec{b}=-u\vec{c}$ と変形して,両辺の大きさの2乗を考える。
\begin{align*}
&\abs{s\vec{a}+t\vec{b}}^2=\abs{-u\vec{c}}^2 \\[4pt]
&s^2\abs{\vec{a}}^2+2st\vec{a}\Cdota\vec{b}+t^2\abs{\vec{b}}^2=u^2\abs{\vec{c}}^2
\end{align*}
この方法では,$\abs{\vec{a}},~\abs{\vec{b}},~\abs{\vec{c}}$ が分かっているときに $\vec{a}\Cdot\vec{b}$ を求めることができる。&\abs{s\vec{a}+t\vec{b}}^2=\abs{-u\vec{c}}^2 \\[4pt]
&s^2\abs{\vec{a}}^2+2st\vec{a}\Cdota\vec{b}+t^2\abs{\vec{b}}^2=u^2\abs{\vec{c}}^2
\end{align*}
② 両辺それぞれと $\vec{a}$ との内積を考える。
\begin{align*}
&(s\vec{a}+t\vec{b}+u\vec{c})\Cdota\vec{a}=\vec{0}\Cdota\vec{a} \\[4pt]
&s\abs{\vec{a}}^2+t\vec{a}\Cdota\vec{b}+u\vec{c}\Cdota\vec{a}=0
\end{align*}
この方法では,$\abs{\vec{a}},~\vec{c}\Cdot\vec{a}$ が分かっているときに $\vec{a}\Cdot\vec{b}$ を求めることができる。$\abs{\vec{b}},~\vec{b}\Cdot\vec{c}$ が分かっているときは,両辺それぞれと $\vec{b}$ との内積を考えればよい。&(s\vec{a}+t\vec{b}+u\vec{c})\Cdota\vec{a}=\vec{0}\Cdota\vec{a} \\[4pt]
&s\abs{\vec{a}}^2+t\vec{a}\Cdota\vec{b}+u\vec{c}\Cdota\vec{a}=0
\end{align*}

ヒロ
このことを知っている状態で問題を考えよう。
【解答と考え方】
$\sankaku{ABC}$ が半径1の円に内接していて,その円の中心がOだから,
$\sankaku{ABC}$ が半径1の円に内接していて,その円の中心がOだから,
\begin{align*}
\textrm{OA}=\textrm{OB}=\textrm{OC}=1
\end{align*}
が成り立つ。与えられた関係式から\textrm{OA}=\textrm{OB}=\textrm{OC}=1
\end{align*}
\begin{align*}
4\Vec{OA}+4\Vec{OB}=-\Vec{OC}
\end{align*}
となる。よって4\Vec{OA}+4\Vec{OB}=-\Vec{OC}
\end{align*}
\begin{align*}
&\abs{4\Vec{OA}+4\Vec{OB}}^2=\abs{-\Vec{OC}}^2 \\[4pt]
&16\abs{\Vec{OA}}^2+32\Vec{OA}\Cdota\Vec{OB}+16\abs{\Vec{OB}}^2=\abs{\Vec{OC}}^2 \\[4pt]
&16+32\Vec{OA}\Cdota\Vec{OB}+16=1 \\[4pt]
&\Vec{OA}\Cdota\Vec{OB}=-\dfrac{31}{32}
\end{align*}
&\abs{4\Vec{OA}+4\Vec{OB}}^2=\abs{-\Vec{OC}}^2 \\[4pt]
&16\abs{\Vec{OA}}^2+32\Vec{OA}\Cdota\Vec{OB}+16\abs{\Vec{OB}}^2=\abs{\Vec{OC}}^2 \\[4pt]
&16+32\Vec{OA}\Cdota\Vec{OB}+16=1 \\[4pt]
&\Vec{OA}\Cdota\Vec{OB}=-\dfrac{31}{32}
\end{align*}

ヒロ
次に $\sankaku{OAB}$ の面積は,$\sankaku{ABC}$ の面積の何倍であるかを求めよう。
【解答と考え方】
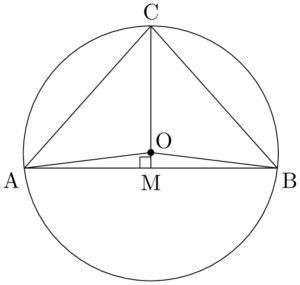
$\sankaku{OAB}$ と $\sankaku{ABC}$ において,ABが共通した辺だからABを底辺と見る。底辺が共通だから,面積比は高さの比と一致する。点O,Cから辺ABに下ろした垂線の足をそれぞれM,Hとすると,$\sankaku{OAB}$ が二等辺三角形であるから,点Mは辺ABの中点である。このとき,
よって,$\sankaku{OAB}$ の面積は,$\sankaku{ABC}$ の面積の $\dfrac{1}{9}$ 倍である。
$\sankaku{OAB}$ と $\sankaku{ABC}$ において,ABが共通した辺だからABを底辺と見る。底辺が共通だから,面積比は高さの比と一致する。点O,Cから辺ABに下ろした垂線の足をそれぞれM,Hとすると,$\sankaku{OAB}$ が二等辺三角形であるから,点Mは辺ABの中点である。このとき,
\begin{align*}
\sankaku{OAB}:\sankaku{ABC}=\textrm{OM}:\textrm{CH}
\end{align*}
となる。ここで,\sankaku{OAB}:\sankaku{ABC}=\textrm{OM}:\textrm{CH}
\end{align*}
\begin{align*}
\Vec{OM}=\dfrac{1}{2}(\Vec{OA}+\Vec{OB})
\end{align*}
であり,$4\Vec{OA}+4\Vec{OB}=-\Vec{OC}$ であるから\Vec{OM}=\dfrac{1}{2}(\Vec{OA}+\Vec{OB})
\end{align*}
\begin{align*}
\Vec{OC}=-8\Vec{OM}
\end{align*}
このことから,点Hは点Mと一致し,\Vec{OC}=-8\Vec{OM}
\end{align*}
\begin{align*}
\textrm{OC}:\textrm{OM}=8:1
\end{align*}
となることが分かる。\textrm{OC}:\textrm{OM}=8:1
\end{align*}

よって,$\sankaku{OAB}$ の面積は,$\sankaku{ABC}$ の面積の $\dfrac{1}{9}$ 倍である。


















