ここでは2次方程式の解の配置問題の典型問題を解説します。
2次方程式の解は2次関数のグラフと $x$ 軸の共有点の $x$ 座標であるため,単に「2次方程式の解」として考えることは少ないです。
ほとんどの場合,2次関数のグラフを利用して考えます。
2次関数のグラフは放物線であり,解の配置問題では次の4つに着目して考えます。
- 上に凸か下に凸か
- 軸の位置(頂点の $x$ 座標)
- 頂点の $y$ 座標(判別式を代用可能)
- 考える範囲の端点の $y$ 座標
問題で与えられた条件を満たすのは,グラフがどのようになるときかを考えましょう。
慣れないうちはかなり難しく感じますが,諦めなければいつかは解けるようになるでしょう。
また,上に凸か下に凸かを意識していないと,グラフが下に凸の放物線として考えてしまい,符号が逆になってしまうことがあるので注意しましょう。
2次方程式の解の配置問題
問題2次方程式 $x^2-mx-m+8=0$ が次のような実数解をもつように,定数 $m$ の値の範囲を定めよ。
(1) 異なる2つの正の解
(2) 異なる2つの負の解
(3) 正の解と負の解
(1) 異なる2つの正の解
(2) 異なる2つの負の解
(3) 正の解と負の解

ヒロ
2次関数 $y=x^2-x-m+8$ のグラフと $x$ 軸の共有点を考えよう。
【(1)の考え方と解答】
条件をみたすのは,2次関数 $C:y=x^2-x-m+8$ のグラフが次のようになるときである。
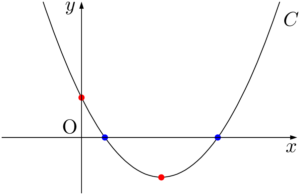
$x^2-mx-m+8=0$ の2解(青丸)がともに正であるための条件を赤丸の頂点と $y$ 切片で考える。
$f(x)=x^2-mx-m+8$ とおくと,条件をみたすのは
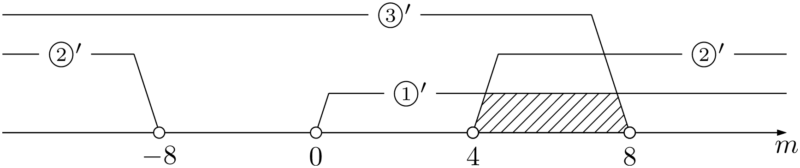
①より,$m>0~\cdots\cdots①’$
②より
条件をみたすのは,2次関数 $C:y=x^2-x-m+8$ のグラフが次のようになるときである。

$x^2-mx-m+8=0$ の2解(青丸)がともに正であるための条件を赤丸の頂点と $y$ 切片で考える。
$f(x)=x^2-mx-m+8$ とおくと,条件をみたすのは
\begin{align*} \begin{cases} 頂点の~x~座標:\dfrac{m}{2}>0 &~\cdots\cdots① \\[4pt] 頂点の~y~座標:f\left(\dfrac{m}{2}\right)<0 &~\cdots\cdots② \\[4pt] y~切片:f(0)>0 &~\cdots\cdots③ \end{cases} \end{align*}
が成り立つときである。①より,$m>0~\cdots\cdots①’$
②より
\begin{align*} &\dfrac{m^2}{4}-\dfrac{m^2}{2}-m+8<0 \\[4pt] &-m^2-4m+32<0 \\[4pt] &m^2+4m-32>0 \\[4pt] &(m+8)(m-4)>0 \\[4pt] &m<-8,~4<m~\cdots\cdots②’ \end{align*}
③より \begin{align*} &-m+8>0 \\[4pt] &m<8~\cdots\cdots③’ \end{align*}
①’,②’,③’より,$4<m<8$
(2) $x^2-mx-m+8=0$ が異なる2つの負の解をもつ
【(2)の考え方と解答】
条件をみたすのは,2次関数 $C:y=x^2-x-m+8$ のグラフが次のようになるときである。
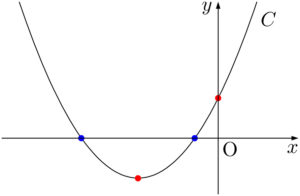
$x^2-mx-m+8=0$ の2解(青丸)がともに正であるための条件を赤丸の頂点と $y$ 切片で考える。
条件をみたすのは
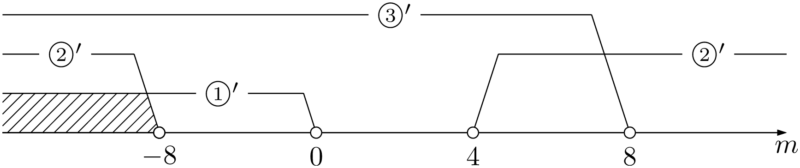
①より,$m<0~\cdots\cdots①’$
②より
条件をみたすのは,2次関数 $C:y=x^2-x-m+8$ のグラフが次のようになるときである。

$x^2-mx-m+8=0$ の2解(青丸)がともに正であるための条件を赤丸の頂点と $y$ 切片で考える。
条件をみたすのは
\begin{align*}
\begin{cases}
頂点の~x~座標:\dfrac{m}{2}<0 &~\cdots\cdots① \\[4pt] 頂点の~y~座標:f\left(\dfrac{m}{2}\right)<0 &~\cdots\cdots② \\[4pt] y~切片:f(0)>0 &~\cdots\cdots③
\end{cases}
\end{align*}
が成り立つときである。\begin{cases}
頂点の~x~座標:\dfrac{m}{2}<0 &~\cdots\cdots① \\[4pt] 頂点の~y~座標:f\left(\dfrac{m}{2}\right)<0 &~\cdots\cdots② \\[4pt] y~切片:f(0)>0 &~\cdots\cdots③
\end{cases}
\end{align*}
①より,$m<0~\cdots\cdots①’$
②より
\begin{align*} &\dfrac{m^2}{4}-\dfrac{m^2}{2}-m+8<0 \\[4pt] &-m^2-4m+32<0 \\[4pt] &m^2+4m-32>0 \\[4pt] &(m+8)(m-4)>0 \\[4pt] &m<-8,~4<m~\cdots\cdots②’ \end{align*}
③より \begin{align*} &-m+8>0 \\[4pt] &m<8~\cdots\cdots③’ \end{align*}
①’,②’,③’より,$m<-8$
(3) $x^2-mx-m+8=0$ が正の解と負の解をもつ
【(3)の考え方と解答】
条件をみたすのは,2次関数 $C:y=x^2-x-m+8$ のグラフが次のようになるときである。
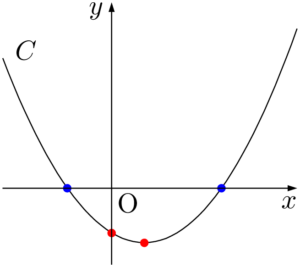
条件をみたすのは
頂点の $x$ 座標(軸の位置)については,正の場合と負の場合があるから考えなくて良い。また,下に凸の放物線であるため,$y$ 切片が負の時点で,頂点の $y$ 座標は必ず負であるため,これも考えなくて良い。
したがって,$f(0)<0$ を解いて,

条件をみたすのは
\begin{align*} y~切片:f(0)<0 \end{align*}
が成り立つときである。頂点の $x$ 座標(軸の位置)については,正の場合と負の場合があるから考えなくて良い。また,下に凸の放物線であるため,$y$ 切片が負の時点で,頂点の $y$ 座標は必ず負であるため,これも考えなくて良い。
したがって,$f(0)<0$ を解いて,
\begin{align*} &-m+8<0 \\[4pt] &m>8 \end{align*}




















