ここでは3つの集合の要素の個数について説明します。
3つの集合の和集合や共通部分などのベン図に慣れていない人は,次の記事から知識を吸収しておきましょう。
2つの集合の要素の個数と比べると,3つの集合の要素の個数はややこしいです。
しかし,落ち着いて考えることで次第に慣れていき解けるようになるでしょう。
3つの集合の和集合の要素の個数

ヒロ
3つの集合の和集合の個数をどのように求めるのかを理解しよう。
3つの集合の和集合の要素の個数全体集合 $U$ の3つの部分集合 $A,~B,~C$ について,それらの和集合の要素の個数は次の式で求められる。
\begin{align*}
n(A\cup B\cup C)&=n(A)+n(B)+n(C) \\[4pt]
& -n(A\cap B)-n(B\cap C)-n(C\cap A) \\[4pt]
& +n(A\cap B\cap C)
\end{align*}
n(A\cup B\cup C)&=n(A)+n(B)+n(C) \\[4pt]
& -n(A\cap B)-n(B\cap C)-n(C\cap A) \\[4pt]
& +n(A\cap B\cap C)
\end{align*}

ヒロ
この式をイメージで理解するなら次のような感じ。
【イメージで理解する】
$A,~B,~C$ の集合を表す円にシールを貼っていくことを想像する。
3つの集合にシールを貼ると,$A$ と $B$ の部分が重なっているから1枚剥がす。
$B$ と $C$,$C$ と $A$ の重なっている部分についても同じように1枚剥がす。
そうすると,3つの集合の共通部分については,最初3枚重なっていて,3枚剥がすと何もない状態になるから,3つの共通部分の形のシールを貼る。
これで3つの集合の和集合にぴったりシールを貼ることができる。

ヒロ
そんなイメージでは理解できないという人は,次のように文字を利用した方法で理解しよう。
【要素の個数を文字でおく】
3つの集合の各部分の要素の個数を次の図のように
\begin{align*}
a,~b,~c,~d,~e,~f,~g
\end{align*}
とする。視認性を高めるために色を付けた。a,~b,~c,~d,~e,~f,~g
\end{align*}
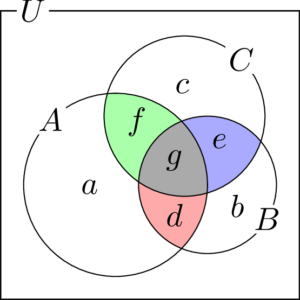
この図より
\begin{align*}
&n(A)=a+d+f+g \\[4pt]
&n(B)=b+d+e+g \\[4pt]
&n(C)=c+e+f+g \\[4pt]
&n(A\cap B)=d+g \\[4pt]
&n(B\cap C)=e+g \\[4pt]
&n(C\cap A)=f+g \\[4pt]
&n(A\cap B\cap C)=g
\end{align*}
となるから&n(A)=a+d+f+g \\[4pt]
&n(B)=b+d+e+g \\[4pt]
&n(C)=c+e+f+g \\[4pt]
&n(A\cap B)=d+g \\[4pt]
&n(B\cap C)=e+g \\[4pt]
&n(C\cap A)=f+g \\[4pt]
&n(A\cap B\cap C)=g
\end{align*}
\begin{align*}
&n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C) \\[4pt]
&=(a+{\color[named]{RubineRed}d}+{\color[named]{Green}f}+{\color[named]{Gray}g})
+(b+{\color[named]{RubineRed}d}+{\color[named]{Blue}e}
+{\color[named]{Gray}g})+(c+{\color[named]{Blue}e}+{\color[named]{Green}f}+{\color[named]{Gray}g})
-({\color[named]{RubineRed}d}+{\color[named]{Gray}g})-({\color[named]{Blue}e}+{\color[named]{Gray}g})
-({\color[named]{Green}f}+{\color[named]{Gray}g})+{\color[named]{Gray}g} \\[4pt]
&=a+b+c+{\color[named]{RubineRed}d}+{\color[named]{Blue}e}+{\color[named]{Green}f}+{\color[named]{Gray}g}
\end{align*}
&n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C) \\[4pt]
&=(a+{\color[named]{RubineRed}d}+{\color[named]{Green}f}+{\color[named]{Gray}g})
+(b+{\color[named]{RubineRed}d}+{\color[named]{Blue}e}
+{\color[named]{Gray}g})+(c+{\color[named]{Blue}e}+{\color[named]{Green}f}+{\color[named]{Gray}g})
-({\color[named]{RubineRed}d}+{\color[named]{Gray}g})-({\color[named]{Blue}e}+{\color[named]{Gray}g})
-({\color[named]{Green}f}+{\color[named]{Gray}g})+{\color[named]{Gray}g} \\[4pt]
&=a+b+c+{\color[named]{RubineRed}d}+{\color[named]{Blue}e}+{\color[named]{Green}f}+{\color[named]{Gray}g}
\end{align*}
3つの集合の要素の個数に関する問題

ヒロ
それでは実際に定期テストで出題された問題を解いてみよう。
問題1から100までの整数のうち,次のような整数は何個あるか。
(1) 3で割り切れる数
(2) 3と7の少なくとも一方で割り切れる数
(3) 2,3,7の少なくとも1つで割り切れる数
(1) 3で割り切れる数
(2) 3と7の少なくとも一方で割り切れる数
(3) 2,3,7の少なくとも1つで割り切れる数

ヒロ
集合を設定して解こう。
【考え方と解答】
1から100までの整数を全体集合 $U$ として,その部分集合として,3で割り切れる数,7で割り切れる数,2で割り切れる数
全体の集合をそれぞれ $A,~B,~C$ とする。
(1) 集合 $A$ の要素は
よって,3で割り切れる数は33個。
(2) 3と7の少なくとも一方で割り切れる数全体の集合は $A\cup B$ であり,その要素の個数は次の式で求められる。
また,$A\cap B$ は3と7の最小公倍数21の倍数全体の集合であるから
したがって
(3) 2,3,7の少なくとも1つで割り切れる数全体の集合は $A\cup B\cup C$ である。
ここで $n(C)=50$ である。また,$B\cap C$ は14で割り切れる数全体の集合であるから,$n(B\cap C)=7$ である。
$C\cap A$ は6で割り切れる数全体の集合であるから,$n(C\cap A)=16$ である。
$A\cap B\cap C$ は42で割り切れる数全体の集合であるから,$n(A\cap B\cap C)=2$ である。
したがって
1から100までの整数を全体集合 $U$ として,その部分集合として,3で割り切れる数,7で割り切れる数,2で割り切れる数
全体の集合をそれぞれ $A,~B,~C$ とする。
(1) 集合 $A$ の要素は
\begin{align*}
A=\{3\Cdota1,~3\Cdota2,~\cdots,~3\Cdota33\}
\end{align*}
となるから,$n(A)=33$ である。A=\{3\Cdota1,~3\Cdota2,~\cdots,~3\Cdota33\}
\end{align*}
よって,3で割り切れる数は33個。
(2) 3と7の少なくとも一方で割り切れる数全体の集合は $A\cup B$ であり,その要素の個数は次の式で求められる。
\begin{align*}
n(A\cup B)=n(A)+n(B)-n(A\cap B)
\end{align*}
ここでn(A\cup B)=n(A)+n(B)-n(A\cap B)
\end{align*}
\begin{align*}
B=\{7\Cdota1,~7\Cdota2,~\cdots,~7\Cdota14\}
\end{align*}
より,$n(B)=14$B=\{7\Cdota1,~7\Cdota2,~\cdots,~7\Cdota14\}
\end{align*}
また,$A\cap B$ は3と7の最小公倍数21の倍数全体の集合であるから
\begin{align*}
A\cap B=\{21\Cdota1,~21\Cdota2,~21\Cdota3,~21\Cdota4\}
\end{align*}
より,$n(A\cap B)=4$A\cap B=\{21\Cdota1,~21\Cdota2,~21\Cdota3,~21\Cdota4\}
\end{align*}
したがって
\begin{align*}
n(A\cup B)=33+14-4=43
\end{align*}
n(A\cup B)=33+14-4=43
\end{align*}
(3) 2,3,7の少なくとも1つで割り切れる数全体の集合は $A\cup B\cup C$ である。
ここで $n(C)=50$ である。また,$B\cap C$ は14で割り切れる数全体の集合であるから,$n(B\cap C)=7$ である。
$C\cap A$ は6で割り切れる数全体の集合であるから,$n(C\cap A)=16$ である。
$A\cap B\cap C$ は42で割り切れる数全体の集合であるから,$n(A\cap B\cap C)=2$ である。
したがって
\begin{align*}
&n(A\cup B\cup C) \\[4pt]
&=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C) \\[4pt]
&=33+14+50-4-7-16+2 \\[4pt]
&=72
\end{align*}
よって,求める個数は72個である。&n(A\cup B\cup C) \\[4pt]
&=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C) \\[4pt]
&=33+14+50-4-7-16+2 \\[4pt]
&=72
\end{align*}
3つの集合の要素の個数に関する問題2

ヒロ
次も定期テストで出題された問題。
問題3桁の自然数のうち,3の倍数全体の集合を $A$,5の倍数の全体の集合を $B$,7の倍数の全体の集合を $C$ とする。3でも5でも7でも割り切れない数は何個あるか。

ヒロ
ド・モルガンの法則と補集合の要素の個数を利用して求めよう。
【考え方と解答】
$n(U)=999-100+1=900$ である。
3でも5でも7でも割り切れない数全体の集合は $\overline{A}\cap\overline{B}\cap\overline{C}$ である。
ド・モルガンの法則と補集合の要素の個数を考えると
$n(U)=999-100+1=900$ である。
3でも5でも7でも割り切れない数全体の集合は $\overline{A}\cap\overline{B}\cap\overline{C}$ である。
ド・モルガンの法則と補集合の要素の個数を考えると
\begin{align*}
&n(\overline{A}\cap\overline{B}\cap\overline{C}) \\[4pt]
&=n(\overline{A\cup B\cup C}) \\[4pt]
&=n(U)-n(A\cup B\cup C)
\end{align*}
ここで&n(\overline{A}\cap\overline{B}\cap\overline{C}) \\[4pt]
&=n(\overline{A\cup B\cup C}) \\[4pt]
&=n(U)-n(A\cup B\cup C)
\end{align*}
\begin{align*}
&A=\{3\Cdota34,~3\Cdota35,~\cdots,~3\Cdota333\} \\[4pt]
&B=\{5\Cdota20,~5\Cdota21,~\cdots,~5\Cdota199\} \\[4pt]
&C=\{7\Cdota15,~7\Cdota16,~\cdots,~7\Cdota142\} \\[4pt]
&A\cap B=\{15\Cdota7,~15\Cdota8,~\cdots,~15\Cdota66\} \\[4pt]
&B\cap C=\{35\Cdota3,~35\Cdota4,~\cdots,~35\Cdota28\} \\[4pt]
&C\cap A=\{21\Cdota5,~21\Cdota6,~\cdots,~21\Cdota47\} \\[4pt]
&A\cap B\cap C=\{42\Cdota3,~42\Cdota4,~\cdots,~42\Cdota23\}
\end{align*}
であるから&A=\{3\Cdota34,~3\Cdota35,~\cdots,~3\Cdota333\} \\[4pt]
&B=\{5\Cdota20,~5\Cdota21,~\cdots,~5\Cdota199\} \\[4pt]
&C=\{7\Cdota15,~7\Cdota16,~\cdots,~7\Cdota142\} \\[4pt]
&A\cap B=\{15\Cdota7,~15\Cdota8,~\cdots,~15\Cdota66\} \\[4pt]
&B\cap C=\{35\Cdota3,~35\Cdota4,~\cdots,~35\Cdota28\} \\[4pt]
&C\cap A=\{21\Cdota5,~21\Cdota6,~\cdots,~21\Cdota47\} \\[4pt]
&A\cap B\cap C=\{42\Cdota3,~42\Cdota4,~\cdots,~42\Cdota23\}
\end{align*}
\begin{align*}
&n(A)=333-34+1=300 \\[4pt]
&n(B)=199-20+1=180 \\[4pt]
&n(C)=142-15+1=128 \\[4pt]
&n(A\cap B)=66-7+1=60 \\[4pt]
&n(B\cap C)=28-3+1=26 \\[4pt]
&n(C\cap A)=47-5+1=43 \\[4pt]
&n(A\cap B\cap C)=23-3+1=21
\end{align*}
したがって&n(A)=333-34+1=300 \\[4pt]
&n(B)=199-20+1=180 \\[4pt]
&n(C)=142-15+1=128 \\[4pt]
&n(A\cap B)=66-7+1=60 \\[4pt]
&n(B\cap C)=28-3+1=26 \\[4pt]
&n(C\cap A)=47-5+1=43 \\[4pt]
&n(A\cap B\cap C)=23-3+1=21
\end{align*}
\begin{align*}
&n(A\cup B\cup C) \\[4pt]
&=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C) \\[4pt]
&=300+180+128-60-26-43+21 \\[4pt]
&=500
\end{align*}
よって,求める個数は&n(A\cup B\cup C) \\[4pt]
&=n(A)+n(B)+n(C)-n(A\cap B)-n(B\cap C)-n(C\cap A)+n(A\cap B\cap C) \\[4pt]
&=300+180+128-60-26-43+21 \\[4pt]
&=500
\end{align*}
\begin{align*}
&n(U)-n(A\cup B\cup C) \\[4pt]
&=900-500=400~個
\end{align*}
&n(U)-n(A\cup B\cup C) \\[4pt]
&=900-500=400~個
\end{align*}