ここでは放物線の弦の中点の軌跡について説明します。
放物線の弦の中点の軌跡を求める問題は,解と係数の関係を利用して軌跡を求める典型問題の1つです。
解と係数の関係をうまく利用できるようにしましょう。
放物線の弦の中点の軌跡【金沢医科大】
2013年 金沢医科大実数 $a$ に対して,直線 $y=ax+2$ を $L$ とし,放物線 $y=\dfrac{3}{2}x^2$ を $C$ とする。このとき,$C$ と $L$ は2点で交わり,その2点を結ぶ線分の中点をMとする。$a$ を変化させたときのMの軌跡を $C_1$ とすれば,$C_1$ を表す方程式は $y=\myBox{ア}\,x^2+\myBox{イ}$ である。
【考え方と解答】
$C$ と $L$ が2点で交わるから
①の2解を $\alpha,~\beta$ とおくと
点Mの座標を $(X,~Y)$ とおくと
よって,求める点Mの軌跡の方程式は
$C$ と $L$ が2点で交わるから
\begin{align*}
&\dfrac{3}{2}x^2-ax-2=0 \\[4pt]
&3x^2-2ax-4=0~\cdots\cdots①
\end{align*}
は異なる2つの実数解をもつ。判別式を $D$ とすると&\dfrac{3}{2}x^2-ax-2=0 \\[4pt]
&3x^2-2ax-4=0~\cdots\cdots①
\end{align*}
\begin{align*}
&D/4=a^2+12>0
\end{align*}
となるから,$a$ の値にかかわらず,$C$ と $L$ は2点で交わる。&D/4=a^2+12>0
\end{align*}
①の2解を $\alpha,~\beta$ とおくと
\begin{align*}
\alpha+\beta=\dfrac{2}{3}a,~\alpha\beta=-\dfrac{4}{3}
\end{align*}
が成り立ち,$C$ と $L$ は2点 $\left(\alpha,~\dfrac{3}{2}\alpha^2\right)$,$\left(\beta,~\dfrac{3}{2}\beta^2\right)$ で交わる。\alpha+\beta=\dfrac{2}{3}a,~\alpha\beta=-\dfrac{4}{3}
\end{align*}
点Mの座標を $(X,~Y)$ とおくと
\begin{align*}
X&=\dfrac{\alpha+\beta}{2}=\dfrac{1}{3}a \cdots\cdots② \\[4pt]
Y&=\dfrac{3}{4}(\alpha^2+\beta^2)=\dfrac{3}{4}\{(\alpha+\beta)^2-2\alpha\beta\} \\[4pt]
&=\dfrac{3}{4}\left\{\left(\dfrac{2}{3}a\right)^2-2\Cdot\left(-\dfrac{4}{3}\right)\right\} \\[4pt]
&=\dfrac{1}{3}a^2+2 \cdots\cdots③
\end{align*}
②より $a=3X$ となり,③に代入するとX&=\dfrac{\alpha+\beta}{2}=\dfrac{1}{3}a \cdots\cdots② \\[4pt]
Y&=\dfrac{3}{4}(\alpha^2+\beta^2)=\dfrac{3}{4}\{(\alpha+\beta)^2-2\alpha\beta\} \\[4pt]
&=\dfrac{3}{4}\left\{\left(\dfrac{2}{3}a\right)^2-2\Cdot\left(-\dfrac{4}{3}\right)\right\} \\[4pt]
&=\dfrac{1}{3}a^2+2 \cdots\cdots③
\end{align*}
\begin{align*}
Y&=\dfrac{1}{3}(3X)^2+2 \\[4pt]
&=3X^2+2
\end{align*}
$a$ がすべての実数値をとるから,$X$ もすべての実数値をとる。Y&=\dfrac{1}{3}(3X)^2+2 \\[4pt]
&=3X^2+2
\end{align*}
よって,求める点Mの軌跡の方程式は
\begin{align*}
y=3x^2+2
\end{align*}
y=3x^2+2
\end{align*}
放物線の弦の中点の軌跡【首都大】
2011年 首都大$k$ を実数とし,曲線 $C_1:y=1-x^2$ と曲線 $C_2:y=x^2-2kx+k^2$ が異なる2点P,Qで交わるとする。以下の問いに答えなさい。
(1) $k$ のとり得る値の範囲を求めなさい。
(2) $k$ の値が変化するとき,線分PQの中点Rの軌跡を図示しなさい。
(1) $k$ のとり得る値の範囲を求めなさい。
(2) $k$ の値が変化するとき,線分PQの中点Rの軌跡を図示しなさい。
【(1)の考え方と解答】
$y=1-x^2$,$y=x^2-2kx+k^2$ を連立して,$y$ を消去すると
$y=1-x^2$,$y=x^2-2kx+k^2$ を連立して,$y$ を消去すると
\begin{align*}
2x^2-2kx+k^2-1=0~\cdots\cdots①
\end{align*}
2曲線 $C_1,~C_2$ が異なる2点で交わるとき,方程式①が異なる2つの実数解をもつ。判別式を $D$ とすると $D>0$ であるから2x^2-2kx+k^2-1=0~\cdots\cdots①
\end{align*}
\begin{align*}
&k^2-2(k^2-1)>0 \\[4pt]
&k^2-2<=0 \\[4pt] &-\sqrt{2}<k<\sqrt{2} \end{align*}
&k^2-2(k^2-1)>0 \\[4pt]
&k^2-2<=0 \\[4pt] &-\sqrt{2}<k<\sqrt{2} \end{align*}
(2) $k$ の値が変化するとき,線分PQの中点Rの軌跡を図示しなさい。
【(2)の考え方と解答】
2点P,Qの $x$ 座標は①の2解である。①の2解を $\alpha,~\beta$ とすると,解と係数の関係より
2点P,Qの $x$ 座標は①の2解である。①の2解を $\alpha,~\beta$ とすると,解と係数の関係より
\begin{align*} \alpha+\beta=k,~\alpha\beta=\dfrac{k^2-1}{2} \end{align*}
が成り立つ。線分PQの中点Rの座標を $(X,~Y)$ とすると \begin{align*} X&=\dfrac{\alpha+\beta}{2}=\dfrac{k}{2} \\[4pt] Y&=\dfrac{(1-\alpha^2)+(1-\beta^2)}{2}=1-\dfrac{\alpha^2+\beta^2}{2} \\[4pt] &=1-\dfrac{(\alpha+\beta)^2-2\alpha\beta}{2} \\[4pt] &=1-\dfrac{k^2-2\Cdot\dfrac{k^2-1}{2}}{2} \\[4pt] &=\dfrac{1}{2} \end{align*}
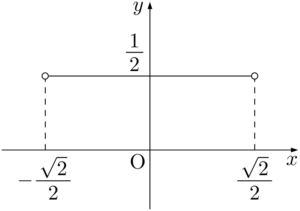
$-\sqrt{2}<k<\sqrt{2}$ のとき,$-\dfrac{\sqrt{2}}{2}<X<\dfrac{\sqrt{2}}{2}$ よって,求める点Rの軌跡は,直線 $y=\dfrac{1}{2}$ の $-\dfrac{\sqrt{2}}{2}<x<\dfrac{\sqrt{2}}{2}$ の部分で,次の図のようになる。


















