ここでは,三角関数を含む方程式の解の個数について説明します。
一般に,方程式の解の個数を求める方法として,次の方法が考えられます。
- 方程式の解を求めて個数を数える。
- グラフを描いて共有点の個数を数える。
解を求めるのは面倒なので,グラフの共有点として解の個数を数えられるなら,その方法が楽でしょう。
Contents
2017年 福岡大
2017年 福岡大・医$\sin\theta=\abs{\cos3\theta}$ をみたすような $0\leqq\theta\leqq\pi$ は全部で $\myhako$ 個ある。
【考え方と解答】
$y=\sin\theta$ と $y=\abs{\cos3\theta}$ のグラフの共有点の個数を調べよう。
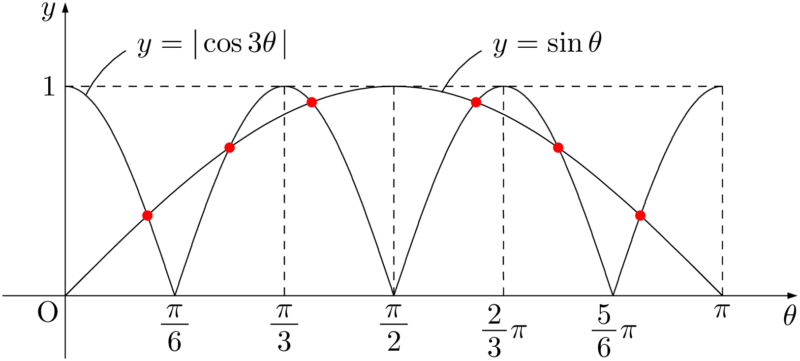
グラフより,方程式をみたす $\theta~(0\leqq\theta\leqq\pi)$ は全部で6個ある。
$y=\sin\theta$ と $y=\abs{\cos3\theta}$ のグラフの共有点の個数を調べよう。

グラフより,方程式をみたす $\theta~(0\leqq\theta\leqq\pi)$ は全部で6個ある。


















