中学校でも関数とグラフについて学んでいるが,高校では様々な関数を扱うことになります。
その中でも特に重要な関数が高校1年生で学習する「二次関数」です。
二次関数のグラフやその後に学ぶ二次方程式で躓いてしまうと,その後に学ぶ様々な関数でも同じように躓いてしまうでしょう。
この記事では二次関数を学ぶ準備として,関数とグラフに関する基礎知識を説明します。
関数とは

中学校で既に習っているが,念のため関数について復習しておこう。
また,関数 $y=f(x)$ において,$x$ の値 $a$ に対応して定まる $y$ の値を $f(a)$ と書き,関数 $f(x)$ の $x=a$ における値という。

例えば,正方形の1辺の長さを $x$ とし,面積を $y$ とすると,$x$ を決めるとそれに対応して $y$ がただ1つ決まるから,$y$ は $x$ の関数である。

関数にならない例としては,身長を $x$ とし,体重を $y$ とする場合がある。身長の $x$ を決めても体重の $y$ は1つに決まらないから,$y$ は $x$ の関数であるとは言えない。

$x$ を決めたときに $y$ がただ1つに決まるかどうかがポイントだね。
定義域と値域

次に定義域と値域について知っておこう。

例えば,関数 $y=3x-2$ の定義域は実数全体である。また,関数 $y=\dfrac{1}{x}$ の定義域は,0以外の実数全体となる。

分母が $x$ を含む式になっているときは,分母が0になるような $x$ の値で $y$ が定義されなくなることを気にするようにしよう。
関数の値を求める問題

それでは定期テストで出題された問題を解いてみよう。
(1) $f(x)=2x+3$ のとき,$f(1)$
(2) $g(x)=x^3-1$ のとき,$g(a+1)$

正確に計算しよう。
$x$ に1を代入して
f(1)=2\Cdota1+3=5
\end{align*}

代入するものが式になることもある。
$x=a+1$ を代入して
g(a+1)&=(a+1)^3-1 \\[4pt]
&=(a^3+3a^2+3a+1)-1 \\[4pt]
&=a^3+3a^2+3a
\end{align*}
座標平面と象限

次は座標平面と象限について知っておこう。
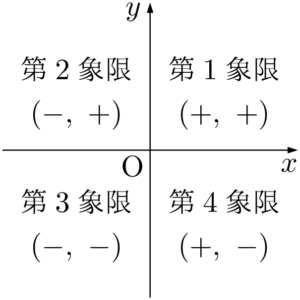
座標軸で分けられた座標平面の4つの部分をそれぞれ,図のように第1象限,第2象限,第3象限,第4象限という。
ただし,座標軸上の点はどの象限にも属さないとする。
なお,図の $(+,~+)$ などは,各象限での $x$ 座標,$y$ 座標の符号を示している。

簡単にチェックしておこう。
(1) $(2,~3)$
(2) $(-1,~-5)$
(3) $(-3,~2)$
(4) $(4,~-3)$
座標平面に点をとって,どの象限にあるかを調べよう。
4点は図のような位置にあるから,答えは次のようになる。
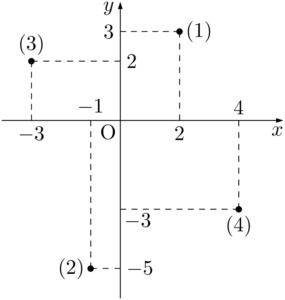
(1) 第1象限
(2) 第3象限
(3) 第2象限
(4) 第4象限
関数のグラフ

関数の値がどのように変化しているかは,座標平面上でグラフを描くとよく分かる。

当たり前のことであるが,次のことは非常に重要である。

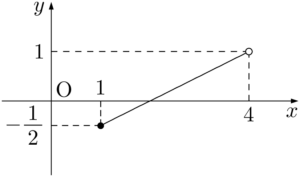
グラフを描くときに端点を含むときは黒丸に,含まないときは白丸にすると良い。
例えば,関数 $y=\dfrac{1}{2}x-1\;(1\leqq x<4)$ のグラフは次のようになる。 図3 この関数の最大値はなく,$x=1$ のとき,最小値 $-\dfrac{1}{2}$ をとる。 最大値がない理由は次の通りである。 $x$ の値を4にすることはできないため,$y$ は1と等しくなることはない。$x$ の値を4より小さい値で「ココ!」と決めたとしても,その値より大きくて4より小さい値を $x$ の値にすることができ,$y$ の値は大きくなる。これを繰り返したとしても,どんどん $y$ の値を大きくすることができるが,ここが最も大きい値だと言える点が存在しないため,最大値は存在しない。