ここでは命題と条件について説明します。
「条件」は日常生活で使っている言葉でもあるため,馴染みがありますが,「命題」が何なのかは分かりにくいかもしれません。
まずは命題とは何かを知ることから始めましょう。
命題が正しいとき,その命題は真であるといい,命題が正しくないとき,その命題は偽であるという。

例えば次の文は命題になる。
- 実数 $x$ について,$x^2\geqq0$ である。
- 偶数は素数ではない。

$x$ が実数のとき,常に $x^2\geqq0$ となるから,①は正しい文,つまり真であるといえるから命題だね。

偶数でも2は素数だから,②は正しくない文,つまり偽であるといえるから,これも命題だね。

答える人によって真偽が変わらない文を命題ということを覚えておこう。

また,命題が偽のとき,その例となるものを反例ということも覚えておこう。
Contents
条件と集合

中学数学でも「条件」という言葉を聞いたことがあるかもしれないけど,一応説明しておこう。

例えば「$x$ は10以下の自然数」のような $x$ を用いて表された文のことだね。

このような条件を考えるときには,「自然数全体を扱う」とか「整数全体を扱う」など,扱う数を予め決めておくべきで,この集合を全体集合ということも覚えておこう。
仮定と結論

命題の多くが次の形式で書かれる。
このとき,条件 $p$ を仮定,条件 $q$ を結論という。

次に命題の真偽と集合の包含関係について理解しよう。
全体集合を $U$ として,命題 $p\Longrightarrow q$ において,条件 $p$ を満たす $U$ の要素全体の集合を $P$,条件 $q$ を満たす $U$ の要素全体の集合を $Q$ とする。
このとき $p\Longrightarrow q$ が真であれば $P\subset Q$ が成り立つ。
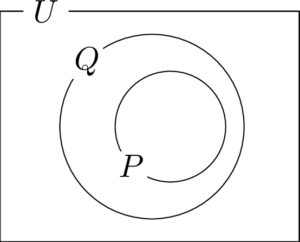

$p\Longrightarrow q$ が真ということは,条件 $p$ を満たすときに,すべて条件 $q$ を満たしているということだから,集合 $P$ の要素はすべて集合 $Q$ に含まれるということになるね。

丸覚えするのではなく,しっかりと意味を理解しよう。
命題の真偽を答える問題

それでは実際に定期テストで出題された問題を解いてみよう。
(1) $x\geqq2\Longrightarrow x\geqq5$
(2) $a^2=2a\Longrightarrow a=2$
(3) $\abs{x}\leqq2\Longrightarrow\abs{x-1}<3$
(4) $ab=0\Longrightarrow a^2+b^2=0$
(5) $a+b,~ab$ がともに有理数 $\Longrightarrow$ $a,~b$ はともに有理数

1つずつ考えていこう。
$x$ が2以上ならば,必ず $x$ が5以上であると言えるかどうかを考える。 言えるなら真,言えなければ偽となる。 それほど難しくないだろう。 $x$ が2以上だからといっても $x=3$ の場合は $x$ が5以上であるとは言えないから偽である。反例は $x=3$

命題が成り立つ(真)かどうかは「必ず」成り立つかどうかを考えよう。


次は方程式を解いて考えよう。
$a^2=2a$ のとき

次は不等式を解いて考えよう。
$\abs{x}\leqq2$ より $-2\leqq x\leqq2$
$\abs{x-1}<3$ より
よって,命題は偽である。反例は $x=-2$

ちょっとややこしい問題。
$ab=0$ のとき $a=0$ または $b=0$ また $a^2+b^2=0$ となるのは $a=0$ かつ $b=0$ のとき。 $a$ と $b$ の少なくとも一方が0以外の値なら成り立たないから,命題は偽である。反例は $a=0,~b=1$ 反例は命題が成り立たない例を1つ挙げれば良いので,$a=-1,~b=0$ 等でも良い。

思い込みを除外して,色々なパターンを考えよう。
$a+b$ と $ab$ がともに有理数なら $a$ と $b$ が有理数と必ず言えるかどうかを考える。 これは有名問題の1つで,命題は偽である。 反例は $a=-\sqrt{2},~b=\sqrt{2}$ このとき $a+b=0,~ab=-2$ となって確かに両方とも有理数だけど,$a$ と $b$ はともに無理数になる。

今後のためにも,命題が真であるか偽であるかを判定することが容易にできる数学力を身に付けておこう。


















