ベクトルの基本は「伸ばす(縮める)」と「つなぐ」です。
しっかり考えることで,どんなベクトルを伸ばして(縮めて)つなぐのかが分かれば,どんなベクトルでも複数のベクトルの和で表すことができます。
ベクトルを伸ばしたり縮めたりする場合,図形に関する知識が重要となります。
ベクトルの問題だからといって,図形の性質を考えることなく,方程式でゴリゴリ解くというのは得策でないかもしれません。
柔軟に考えることができるように,普段から様々な単元の知識をリンクすることが大切です。
2018年 千葉大

それでは次の問題を解いてみよう。
(1) $\alpha=\dfrac{\abs{\Vec{PB}}}{\abs{\Vec{PA}}}$とするとき,$x,~y$ を $\alpha$ を用いて表せ。
(2) 点Pが題意の条件を満たしながら動くとき,(1)で求めた $x,~y$ の和 $x+y$ の最大値を求め,そのときのPがどのような点かを答えよ。
(1)の考え方と解答

とりあえず正方形ABCDの内部に条件を満たすような点Pをとって考えよう。
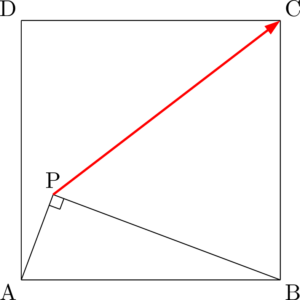

図の赤いベクトルを $\Vec{PA}$ と $\Vec{PB}$ で表したいのだから,その2方向に分解して考えよう。
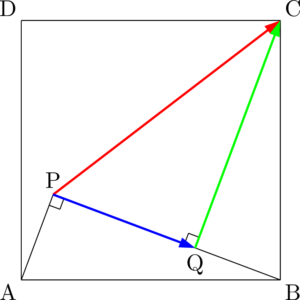

この図を見て $\Vec{PC}$ を複数のベクトルの和で表すとどうなる?

$\Vec{PC}=\Vec{PQ}+\Vec{QC}$ になります。

そうだね。では,$x,~y$ を求めるためには,$\mathrm{AP:QC}$ と $\mathrm{PQ:QB}$ が分かれば良いね。

そうですね。

また,この図を見てあることに気付かなければならない。それは何か分かるかな?

$\sankaku{ABP}$ と $\sankaku{BCQ}$ が合同な2つの三角形だと分かります。

そこまで分かればもう解けるね。
点Cから線分BPに下ろした垂線の足をQとすると,$\sankaku{ABP}\equiv\sankaku{BCQ}$ である。
$\alpha=\dfrac{\abs{\Vec{PB}}}{\abs{\Vec{PA}}}$ より,$\mathrm{AP:BP}=1:\alpha$ である。$\mathrm{AP=BQ}$ だから,$\mathrm{AP:PQ}=1:(\alpha-1)$ である。
さらに,$\mathrm{BP=CQ}$ より,$\mathrm{AP:CQ}=1:\alpha$ であるから,
\Vec{PC}&=\Vec{PQ}+\Vec{QC} \\
&=\dfrac{\alpha-1}{\alpha}\Vec{PB}-\alpha\Vec{PA}
\end{align*}
x=-\alpha,~y=\dfrac{\alpha-1}{\alpha}
\end{align*}
(2)の考え方と解答
(2) 点Pが題意の条件を満たしながら動くとき,(1)で求めた $x,~y$ の和 $x+y$ の最大値を求め,そのときのPがどのような点かを答えよ。

とりあえず $x+y$ を $\alpha$ で表してみよう。

$x+y=-\alpha+\dfrac{\alpha-1}{\alpha}$ となります。

ここから,どう変形していくかが重要だね。

分数式の変形の原則は何だったかな?

分子の低次化です。

そうだね。分数式では分子の次数が分母の次数より低くなるように変形するのが基本だったね。

ということは,$x+y=-\alpha+1-\dfrac{1}{\alpha}$ となりますね。

ここまで変形すれば分かりやすい形になってるね。

相加・相乗平均の関係ですね!

そうだね。
$\alpha>0$ のとき,相加・相乗平均の関係より,
\alpha+\dfrac{1}{\alpha}&\geqq2\sqrt{\alpha\cdot\dfrac{1}{\alpha}} \\[4pt]
&=2(等号成立は~\alpha=1~のとき)
\end{align*}
x+y=1-\left(\alpha+\dfrac{1}{\alpha}\right)\leqq-1
\end{align*}
であるから,$\sankaku{ABP}$ は直角二等辺三角形である。つまり,点Pは正方形ABCDの対角線の交点である。
したがって,$x+y$ の最大値は $-1$ であり,このときの点Pは正方形ABCDの対角線の交点である。


















