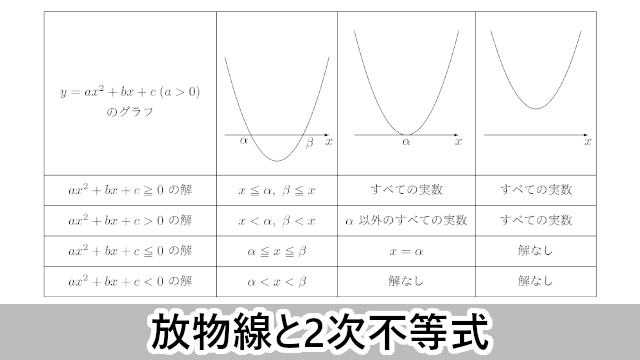
ここでは2次関数のグラフと2次不等式について説明します。
2次不等式を満たすかどうかを2次関数のグラフで見ることができるようになりましょう。
意味を理解せず,不等号の向きだけで解くこともできますが,しっかりと意味を理解することで無駄な暗記から解放されます。
覚えるべきことと覚えなくても良いことを区別できると楽になるでしょう。
Contents
2次関数のグラフと2次不等式の関係

2次不等式の形は次のように分類される。
- $ax^2+bx+c>0$
- $ax^2+bx+c\geqq0$
- $ax^2+bx+c<0$
- $ax^2+bx+c\leqq0$
※両辺に $-1$ をかけることで不等号の向きを逆にする場合は,①と②の2つの形しか存在しないことになる。

例として次の問題を考えよう。

不等式とグラフの関係に着目しよう。
求める解は「与えられた不等式を満たす $x$ の値の範囲」であり,グラフで考えると $y=x^2-2x-3$ のグラフが $x$ 軸の上(共有点を含む)になる $x$ 座標の範囲である。$x^2-2x-3=(x-3)(x+1)$ と因数分解できることを考えると,$y=x^2-2x-3$ のグラフと $x$ 軸の共有点は $(-1,~0)$, $(3,~0)$ であるから,グラフは次のようになる。
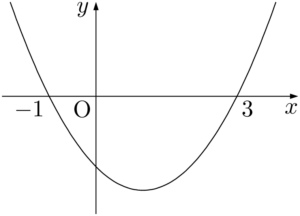
放物線が $x$ 軸より上(共有点を含む)になる部分を赤線で表すと次のようになる。
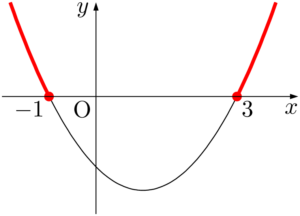
赤線で示した放物線の $x$ 座標だけに着目すると次のようになる。
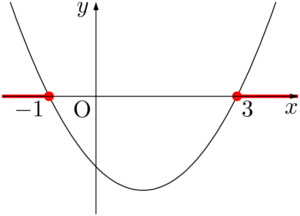
したがって,不等式の解は $x\leqq-1,~3\leqq x$ となる。

他のタイプも解いておこう。
(1) $x^2-2x-3>0$
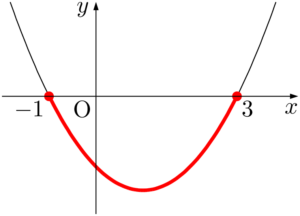
(2) $x^2-2x-3\leqq0$
(3) $x^2-2x-3<0$

グラフを見て解こう。
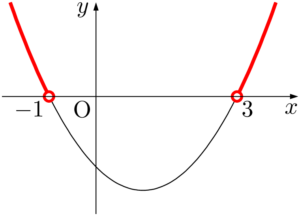
(2) $x^2-2x-3\leqq0$
$x$ 軸に接する2次関数と2次不等式の関係

それでは色々な2次不等式を解いていこう。
(1) $x^2-2x+1\geqq0$
(2) $x^2-2x+1>0$
(3) $x^2-2x+1\leqq0$
(4) $x^2-2x+1<0$

2次関数のグラフを描いて条件を満たす $x$ の値の範囲を考えよう。
$y=x^2-2x+1=(x-1)^2$ のグラフは点 $(1,~0)$ で $x$ 軸に接する下に凸の放物線である。$y$ 座標が0以上になる部分は赤線部分,すなわち放物線全体である。
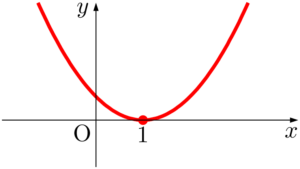
したがって,不等式の解は「すべての実数」となる。

不等式の解が「すべての実数」となることが微妙に感じる人もいるかもしれない。

しかし,不等式の解は「不等式を満たす $x$ の値の範囲」であるから,こういうこともある。
(2) $x^2-2x+1>0$
$y=x^2-2x+1$ のグラフで $y$ 座標が正になる部分は赤線部分,すなわち放物線全体から点 $(1,~0)$ を除いたものである。
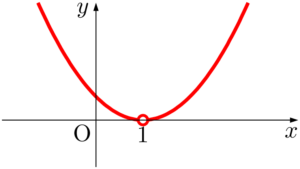
したがって,不等式の解は「1以外のすべての実数」となる。
(3) $x^2-2x+1\leqq0$
$y=x^2-2x+1$ のグラフで $y$ 座標が0以下になる部分は点 $(1,~0)$ のみである。
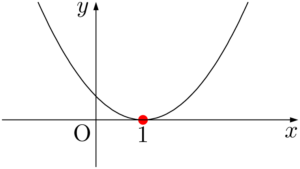
したがって,不等式の解は「$x=1$」となる。

このように,不等式の解が等式で表されることもある。
(4) $x^2-2x+1<0$
$y=x^2-2x+1$ のグラフで $y$ 座標が負になる部分は存在しない。
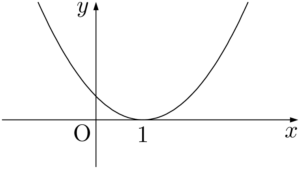
したがって,不等式の解は「解なし」となる。

このように,不等式の解が存在しないこともある。
$x$ 軸と共有点をもたない2次関数と2次不等式の関係
(1) $x^2-4x+5\geqq0$
(2) $x^2-4x+5>0$
(3) $x^2-4x+5\leqq0$
(4) $x^2-4x+5<0$

2次関数のグラフを描いて条件を満たす $x$ の値の範囲を考えよう。
$y=x^2-4x+5=(x-2)^2+1$ のグラフは $x$ 軸と共有点をもたない下に凸の放物線である。$y$ 座標が0以上になる部分は赤線部分,すなわち放物線全体である。
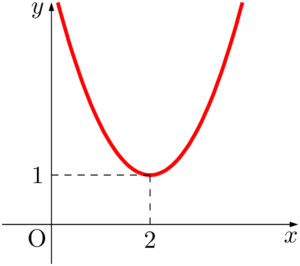
したがって,不等式の解は「すべての実数」となる。
(2) $x^2-4x+5>0$
$y=x^2-2x+1$ のグラフで $y$ 座標が正になる部分は(1)と同様に,放物線全体である。
したがって,不等式の解は「すべての実数」となる。
(3) $x^2-4x+5\leqq0$
$y=x^2-4x+5$ のグラフで $y$ 座標が0以下になる部分は存在しない。
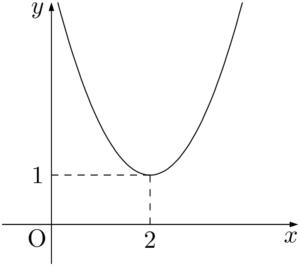
したがって,不等式の解は「解なし」となる。

このように,不等式の解が等式で表されることもある。
(4) $x^2-4x+5<0$
$y=x^2-2x+1$ のグラフで $y$ 座標が負になる部分は存在しない。したがって,不等式の解は「解なし」となる。
2次関数のグラフと2次不等式の関係のまとめ

2次関数のグラフと2次不等式の関係をまとめると次のようになる。


この表を覚えようとする人がいるけど,それは間違っている。

理解していれば覚える必要などないはずである。

あくまでも,2次関数のグラフと2次不等式の関係をまとめると,このようになるというだけである。