ここでは絶対値を含む方程式の解法について説明します。
「絶対値」を見るだけで拒絶反応を起こして諦めないようにしましょう。
場合分けの方法を知って,しっかり取り組むことで必ず解けるようになります。
それでは実際に定期テストで出題された問題を扱って説明していきます。
定期テストに出題された問題1

ヒロ
それでは次の問題を考えてみよう。
問題1方程式 $\abs{x-1}=2x$ を解け。

ヒロ
絶対値記号は,その中身が0以上ならそのままで,負なら正に変えるという役割をもつことは知っておこう。
場合分けをする解法

ヒロ
この問題では絶対値の中身が $x-1$ という文字で表された式のため,$x$ の値の範囲によって符号が変わるね。

ということは場合分けですね!

ヒロ
その方針で解いてみよう。
【問題1の考え方と解法】
$x-1$ が0以上のときと負のときの2通りに分けて考えよう。
(i) $x-1\geqq0$ すなわち $x\geqq1$ のとき
$\abs{x-1}=x-1$ であるから
(ii) $x-1<0$ すなわち $x<1$ のとき $\abs{x-1}=-x+1$ であるから
(i),(ii)より $x=\dfrac{1}{3}$
$x-1$ が0以上のときと負のときの2通りに分けて考えよう。
(i) $x-1\geqq0$ すなわち $x\geqq1$ のとき
$\abs{x-1}=x-1$ であるから
\begin{align*}
&x-1=2x \\[4pt]
&x=-1
\end{align*}
これは $x\geqq1$ を満たさないから不適。&x-1=2x \\[4pt]
&x=-1
\end{align*}
(ii) $x-1<0$ すなわち $x<1$ のとき $\abs{x-1}=-x+1$ であるから
\begin{align*} &-x+1=2x \\[4pt] &x=\dfrac{1}{3} \end{align*}
これは $x<1$ を満たす。(i),(ii)より $x=\dfrac{1}{3}$
グラフを利用する解法
方程式 $\abs{x-1}=2x$ を解け。

ヒロ
グラフを利用する解法を紹介しておこう。

ヒロ
絶対値がついた関数のグラフを習ってないかもしれないが,絶対値を外せるということは $x$ の値の範囲に応じて式が分かっているわけだから,グラフを描くための知識はすでにあることになるね。
【$y=\abs{x}$ のグラフ】
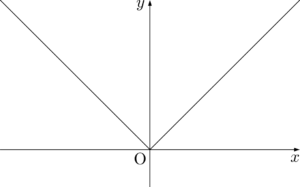
例えば $y=\abs{x}$ のグラフを描くことを考える。
繰り返すことになるが,絶対値記号は0以上ならそのまま,負なら正にする記号だから,グラフの場合は $x$ 軸より下側の部分を $x$ 軸に関して折り返せば良いことになる。つまり $y=x$ のグラフのうち $x$ 軸より下側の部分を折り返して次のようになる。
【グラフを利用した解法】
$y=\abs{x-3}$ のグラフと $y=2x$ のグラフを描くと次のようになる。
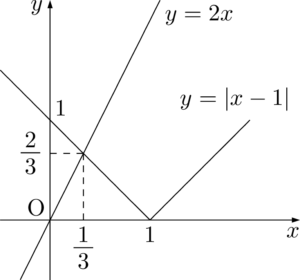
$y=\abs{x-1}$ のグラフと $y=2x$ のグラフの共有点の $x$ 座標が求める解である。すなわち,
$y=\abs{x-3}$ のグラフと $y=2x$ のグラフを描くと次のようになる。

$y=\abs{x-1}$ のグラフと $y=2x$ のグラフの共有点の $x$ 座標が求める解である。すなわち,
\begin{align*}
\begin{cases}
y=-x+1 \\[4pt]
y=2x
\end{cases}
\end{align*}
の解であるから\begin{cases}
y=-x+1 \\[4pt]
y=2x
\end{cases}
\end{align*}
\begin{align*}
&-x+1=2x \\[4pt]
&x=\dfrac{1}{3}
\end{align*}
&-x+1=2x \\[4pt]
&x=\dfrac{1}{3}
\end{align*}
定期テストに出題された問題2

ヒロ
それでは次の問題を考えてみよう。
問題2方程式 $2\abs{x-2}-10=3x-2\abs{x}$ を解け。
場合分けをする解法

ヒロ
絶対値が2つあるときの場合分けの方法については次の記事で説明している。

ヒロ
3通りに場合分けをして,丁寧に解いていこう。
【問題2の考え方と解答】
(i) $x<0$ のとき $\abs{x-2}=-x+2$,$\abs{x}=-x$ であるから
(ii) $0\leqq x<2$ のとき $\abs{x-2}=-x+2$,$\abs{x}=x$ であるから
(iii) $2\leqq x$ のとき $\abs{x-2}=x-2$,$\abs{x}=x$ であるから
(i),(ii),(iii)より $x=-\dfrac{6}{7},~14$
(i) $x<0$ のとき $\abs{x-2}=-x+2$,$\abs{x}=-x$ であるから
\begin{align*} &2(-x+2)-10=3x-2\Cdota(-x) \\[4pt] &-2x-6=5x \\[4pt] &x=-\dfrac{6}{7} \end{align*}
これは $x<0$ を満たす。(ii) $0\leqq x<2$ のとき $\abs{x-2}=-x+2$,$\abs{x}=x$ であるから
\begin{align*} &2(-x+2)-10=3x-2x \\[4pt] &-2x-6=x \\[4pt] &x=-2 \end{align*}
これは $0\leqq x<2$ を満たさないから不適。(iii) $2\leqq x$ のとき $\abs{x-2}=x-2$,$\abs{x}=x$ であるから
\begin{align*} &2(x-2)-10=3x-2x \\[4pt] &2x-14=x \\[4pt] &x=14 \end{align*}
これは $2\leqq x$ を満たす。(i),(ii),(iii)より $x=-\dfrac{6}{7},~14$
グラフを利用する解法
方程式 $2\abs{x-2}-10=3x-2\abs{x}$ を解け。

ヒロ
方程式の解は2つのグラフの共有点の $x$ 座標であることを考えて解いてみよう。
【問題2の別解】
$2\abs{x-2}-10=3x-2\abs{x}$ より
$f(x)$ の $x$ の係数は次のようになる。

したがって,求める解は $x=-\dfrac{6}{7},~14$
$2\abs{x-2}-10=3x-2\abs{x}$ より
\begin{align*}
2\abs{x-2}+2\abs{x}-3x-10=0
\end{align*}
ここで左辺を $f(x)$ として $y=f(x)$ のグラフを考える。2\abs{x-2}+2\abs{x}-3x-10=0
\end{align*}
$f(x)$ の $x$ の係数は次のようになる。
\begin{align*}
\begin{array}{c|c|c|c|c|c}
x & \cdots & 0 & \cdots & 2 & \cdots \\[4pt]\hline
x~の係数 & -7 & & -3 & & 1
\end{array}
\end{align*}
また,\begin{array}{c|c|c|c|c|c}
x & \cdots & 0 & \cdots & 2 & \cdots \\[4pt]\hline
x~の係数 & -7 & & -3 & & 1
\end{array}
\end{align*}
\begin{align*}
&f(0)=4-10=-6 \\[4pt]
&f(2)=4-6-10=-12
\end{align*}
であるから $y=f(x)$ のグラフは次のようになる。&f(0)=4-10=-6 \\[4pt]
&f(2)=4-6-10=-12
\end{align*}

したがって,求める解は $x=-\dfrac{6}{7},~14$
【共有点の $x$ 座標について】
$y=f(x)$ のグラフと $x$ 軸との共有点の $x$ 座標は
\begin{align*}
-7x-6=0,~(x-2)-12=0
\end{align*}
を解いて求めている。-7x-6=0,~(x-2)-12=0
\end{align*}

ヒロ
直線の傾きと通る1点が分かれば,その直線を描けることを利用している。

ヒロ
絶対値を含む方程式をしっかり解けるようにしておこう。



















