ここでは三角形や多角形の面積について説明します。
三角形の面積は小学校で学ぶように「底辺掛ける高さ割る2」で求めることができます。
基本は変わりませんが,三角比を利用することで別の条件が与えられたときの三角形の面積を求めることができるようになります。
三角形の面積

ヒロ
三角形の面積を2辺の長さとその間の角を用いて表すことを考えよう。
【三角形の面積】
$\sankaku{ABC}$ の頂点Cから辺ABまたはその延長に下ろした垂線をCHとする。
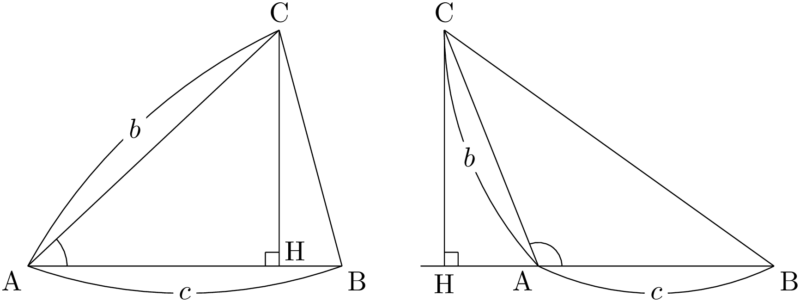
$A$ が鋭角・直角・鈍角にかかわらず,
よって,三角形ABCの面積を $S$ とすると
$\sankaku{ABC}$ の頂点Cから辺ABまたはその延長に下ろした垂線をCHとする。

$A$ が鋭角・直角・鈍角にかかわらず,
\begin{align*}
\text{CH}=\text{AC}\sin A=b\sin A
\end{align*}
と表される。\text{CH}=\text{AC}\sin A=b\sin A
\end{align*}
よって,三角形ABCの面積を $S$ とすると
\begin{align*}
S&=\dfrac{1}{2}\text{AB}\Cdota\text{CH} \\[4pt]
&=\dfrac{1}{2}c\Cdota b\sin A \\[4pt]
&=\dfrac{1}{2}bc\sin A
\end{align*}
S&=\dfrac{1}{2}\text{AB}\Cdota\text{CH} \\[4pt]
&=\dfrac{1}{2}c\Cdota b\sin A \\[4pt]
&=\dfrac{1}{2}bc\sin A
\end{align*}
三角形の面積$\sankaku{ABC}$ の面積を $S$ とすると
\begin{align*}
S&=\dfrac{1}{2}bc\sin A \\[4pt]
&=\dfrac{1}{2}ca\sin B \\[4pt]
&=\dfrac{1}{2}ab\sin C
\end{align*}
S&=\dfrac{1}{2}bc\sin A \\[4pt]
&=\dfrac{1}{2}ca\sin B \\[4pt]
&=\dfrac{1}{2}ab\sin C
\end{align*}

ヒロ
ちなみに,正三角形については面積公式を覚えておいても良いだろう。
正三角形の面積1辺の長さが $a$ の正三角形の面積 $S$ は
\begin{align*}
S=\dfrac{\sqrt{3}}{4}a^2
\end{align*}
となる。S=\dfrac{\sqrt{3}}{4}a^2
\end{align*}
三角形の面積を求める問題

ヒロ
三角形の面積を求める練習をしよう。
問題次のような $\sankaku{ABC}$ の面積 $S$ を求めよ。
(1) $a=3,~c=8,~B=60\Deg$
(2) $a=\sqrt{6},~b=2\sqrt{2},~C=150\Deg$
(1) $a=3,~c=8,~B=60\Deg$
(2) $a=\sqrt{6},~b=2\sqrt{2},~C=150\Deg$
【(1)の考え方と解答】
$\sankaku{ABC}$ は次のようになっている。
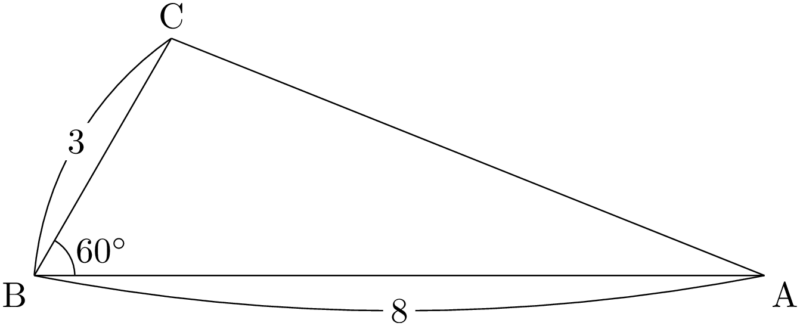
公式を利用すると
$\sankaku{ABC}$ は次のようになっている。

公式を利用すると
\begin{align*}
S&=\dfrac{1}{2}\text{AB}\Cdota\text{BC}\sin\kaku{ABC} \\[4pt]
&=\dfrac{1}{2}\Cdota8\Cdota3\sin60\Deg \\[4pt]
&=6\sqrt{3}
\end{align*}
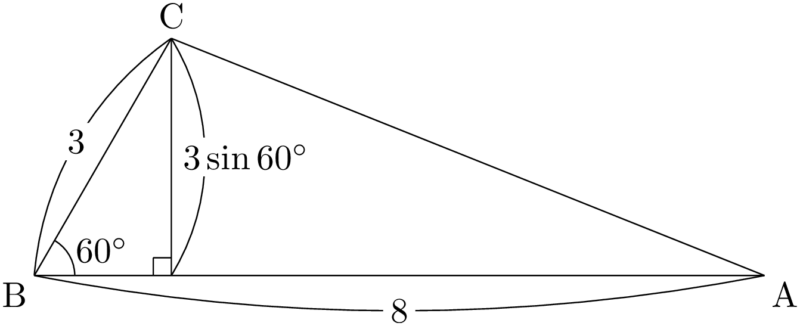
公式を丸覚えすることでも,上のように三角形の面積を求めることはできるが,結局は次の図のように「$\dfrac{1}{2}\times$ 底辺 $\times$ 高さ」であることを時々で良いので意識すると良いだろう。S&=\dfrac{1}{2}\text{AB}\Cdota\text{BC}\sin\kaku{ABC} \\[4pt]
&=\dfrac{1}{2}\Cdota8\Cdota3\sin60\Deg \\[4pt]
&=6\sqrt{3}
\end{align*}

(2) $a=\sqrt{6},~b=2\sqrt{2},~C=150\Deg$
【(2)の考え方と解答】
$\sankaku{ABC}$ は次のようになっている。
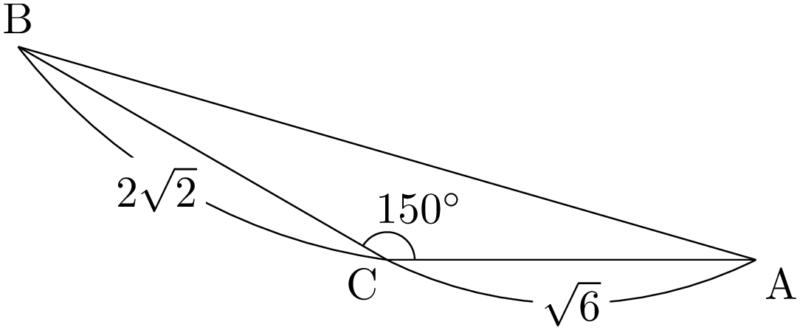

\begin{align*}
S&=\dfrac{1}{2}\text{CA}\Cdota\text{BC}\sin150\Deg \\[4pt]
&=\dfrac{1}{2}\Cdota\sqrt{6}\Cdota2\sqrt{2}\sin150\Deg \\[4pt]
&=\sqrt{3}
\end{align*}
S&=\dfrac{1}{2}\text{CA}\Cdota\text{BC}\sin150\Deg \\[4pt]
&=\dfrac{1}{2}\Cdota\sqrt{6}\Cdota2\sqrt{2}\sin150\Deg \\[4pt]
&=\sqrt{3}
\end{align*}
三角形の面積を求める問題2

ヒロ
三角比を利用することで,3辺の長さから面積を求めることができるようになる。
問題$\sankaku{ABC}$ において,$a=5,~b=6,~c=7$ のとき,この三角形の面積 $S$ を求めよ。
【考え方と解答】
3つの内角の1つのサインを求めよう。そのために,まずは余弦定理でコサインを求めよう。
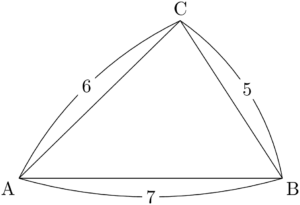
ちなみに3つの角のうち,コサインを求めるのはどれでも良い。今回は $\cos A$ を求めることにする。
3つの内角の1つのサインを求めよう。そのために,まずは余弦定理でコサインを求めよう。

ちなみに3つの角のうち,コサインを求めるのはどれでも良い。今回は $\cos A$ を求めることにする。
\begin{align*}
\cos A&=\dfrac{6^2+7^2-5^2}{2\Cdot6\Cdot7} \\[4pt]
&=\dfrac{60}{2\Cdot6\Cdot7}=\dfrac{5}{7}
\end{align*}
$\sin A>0$ であるから\cos A&=\dfrac{6^2+7^2-5^2}{2\Cdot6\Cdot7} \\[4pt]
&=\dfrac{60}{2\Cdot6\Cdot7}=\dfrac{5}{7}
\end{align*}
\begin{align*}
\sin A&=\sqrt{1-\cos^2A} \\[4pt]
&=\sqrt{1-\left(\dfrac{5}{7}\right)^2} \\[4pt]
&=\dfrac{2\sqrt{6}}{7}
\end{align*}
したがって\sin A&=\sqrt{1-\cos^2A} \\[4pt]
&=\sqrt{1-\left(\dfrac{5}{7}\right)^2} \\[4pt]
&=\dfrac{2\sqrt{6}}{7}
\end{align*}
\begin{align*}
S&=\dfrac{1}{2}\Cdota7\Cdota6\Cdota\dfrac{2\sqrt{6}}{7} \\[4pt]
&=6\sqrt{6}
\end{align*}
S&=\dfrac{1}{2}\Cdota7\Cdota6\Cdota\dfrac{2\sqrt{6}}{7} \\[4pt]
&=6\sqrt{6}
\end{align*}
多角形の面積

ヒロ
四角形や五角形などの多角形の面積を求める方法を知ろう。
多角形の面積多角形の面積を求めるときは三角形に分割して求める。
問題半径1の円に内接する正八角形の面積 $S$ を求めよ。
【考え方と解答】
次の図のように,半径1の円に内接する正八角形を8等分して,$\sankaku{OAB}$ の面積を考える。
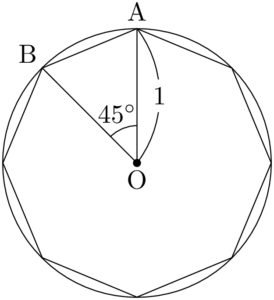
$\kaku{AOB}=45\Deg$ であるから
次の図のように,半径1の円に内接する正八角形を8等分して,$\sankaku{OAB}$ の面積を考える。

$\kaku{AOB}=45\Deg$ であるから
\begin{align*}
\sankaku{OAB}&=\dfrac{1}{2}\Cdota1^2\Cdota\sin45\Deg \\[4pt]
&=\dfrac{\sqrt{2}}{4}
\end{align*}
したがって\sankaku{OAB}&=\dfrac{1}{2}\Cdota1^2\Cdota\sin45\Deg \\[4pt]
&=\dfrac{\sqrt{2}}{4}
\end{align*}
\begin{align*}
S&=\sankaku{OAB}\times8 \\[4pt]
&=\dfrac{\sqrt{2}}{4}\times8=2\sqrt{2}
\end{align*}
S&=\sankaku{OAB}\times8 \\[4pt]
&=\dfrac{\sqrt{2}}{4}\times8=2\sqrt{2}
\end{align*}
多角形の面積を求める問題
問題1辺の長さが1の正十二角形の面積 $S$ を求めよ。
【考え方と解答】
次の図のように,正十二角形を12等分して $\sankaku{OAB}$ の面積を考える。
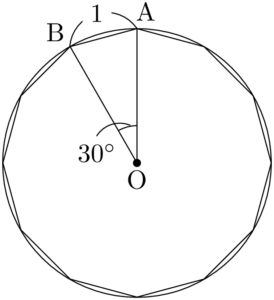
$\sankaku{OAB}$ の面積を求めるために,OAの長さを求める。
$\kaku{AOB}=30\Deg$ であることが分かるから,余弦定理でOAを求めよう。
$\text{OA}=r$ とすると
次の図のように,正十二角形を12等分して $\sankaku{OAB}$ の面積を考える。

$\sankaku{OAB}$ の面積を求めるために,OAの長さを求める。
$\kaku{AOB}=30\Deg$ であることが分かるから,余弦定理でOAを求めよう。
$\text{OA}=r$ とすると
\begin{align*}
&r^2+r^2-2r^2\cos30\Deg=1^2 \\[4pt]
&(2-\sqrt{3})r^2=1 \\[4pt]
&r^2=\dfrac{1}{2-\sqrt{3}}=2+\sqrt{3}
\end{align*}
したがって,$\sankaku{OAB}$ の面積は&r^2+r^2-2r^2\cos30\Deg=1^2 \\[4pt]
&(2-\sqrt{3})r^2=1 \\[4pt]
&r^2=\dfrac{1}{2-\sqrt{3}}=2+\sqrt{3}
\end{align*}
\begin{align*}
\sankaku{OAB}&=\dfrac{1}{2}\text{OA}^2\sin30\Deg \\[4pt]
&=\dfrac{1}{2}r^2\sin30\Deg \\[4pt]
&=\dfrac{1}{4}r^2=\dfrac{2+\sqrt{3}}{4}
\end{align*}
よって,求める正十二角形の面積 $S$ は\sankaku{OAB}&=\dfrac{1}{2}\text{OA}^2\sin30\Deg \\[4pt]
&=\dfrac{1}{2}r^2\sin30\Deg \\[4pt]
&=\dfrac{1}{4}r^2=\dfrac{2+\sqrt{3}}{4}
\end{align*}
\begin{align*}
S&=\sankaku{OAB}\times12 \\[4pt]
&=\dfrac{2+\sqrt{3}}{4}\times12 \\[4pt]
&=3(2+\sqrt{3})
\end{align*}
S&=\sankaku{OAB}\times12 \\[4pt]
&=\dfrac{2+\sqrt{3}}{4}\times12 \\[4pt]
&=3(2+\sqrt{3})
\end{align*}

ヒロ
今回は正十二角形の面積を求めれば良いため,$r^2$ を求めれば良かったが,OAの長さを求める場合は,二重根号を外す必要がある。

ヒロ
$\sqrt{2+\sqrt{3}}$ は二重根号を外せる形であるが,二重根号を外せるかどうかの判断をできるようにしよう。
多角形の面積を求める問題2
問題$\text{AB}=6$, $\text{BC}=10$, $\text{CD}=5$, $\kaku{B}=\kaku{C}=60\Deg$ の四角形ABCDの面積 $S$ を求めよ。
【考え方と解答】
四角形を求めるときは三角形に分割するが,図を描くときも形が分かる三角形を探して,その部分から描くようにしよう。与えられている条件をよく見ると,$\sankaku{BCD}$ の2辺とその間の角が与えられていることが分かる。$1:2:\sqrt{3}$ の直角三角形を描こう。
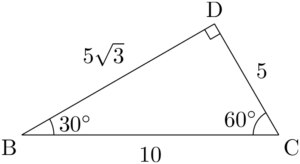
この時点で $\sankaku{BCD}$ の面積を求めることができる。
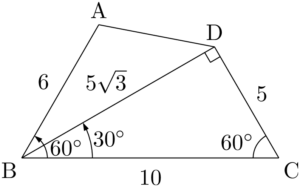
$\kaku{ABD}=60\Deg-30\Deg=30\Deg$ であるから,$\sankaku{ABD}$ の面積を求めることができる。
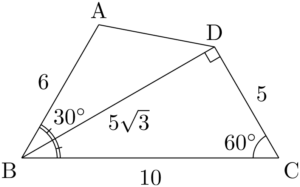
四角形を求めるときは三角形に分割するが,図を描くときも形が分かる三角形を探して,その部分から描くようにしよう。与えられている条件をよく見ると,$\sankaku{BCD}$ の2辺とその間の角が与えられていることが分かる。$1:2:\sqrt{3}$ の直角三角形を描こう。

この時点で $\sankaku{BCD}$ の面積を求めることができる。
\begin{align*}
\sankaku{BCD}=\dfrac{1}{2}\Cdota5\Cdota5\sqrt{3}=\dfrac{25\sqrt{3}}{2}
\end{align*}
$\kaku{B}=60\Deg$ であることと $\text{AB}=6$ であることから点Aの位置が決まる。\sankaku{BCD}=\dfrac{1}{2}\Cdota5\Cdota5\sqrt{3}=\dfrac{25\sqrt{3}}{2}
\end{align*}

$\kaku{ABD}=60\Deg-30\Deg=30\Deg$ であるから,$\sankaku{ABD}$ の面積を求めることができる。

\begin{align*}
\sankaku{ABD}&=\dfrac{1}{2}\Cdota\text{BD}\Cdota\text{BA}\sin30\Deg \\[4pt]
&=\dfrac{1}{2}\Cdota5\sqrt{3}\Cdota6\Cdota\dfrac{1}{2} \\[4pt]
&=\dfrac{15\sqrt{3}}{2}
\end{align*}
したがって\sankaku{ABD}&=\dfrac{1}{2}\Cdota\text{BD}\Cdota\text{BA}\sin30\Deg \\[4pt]
&=\dfrac{1}{2}\Cdota5\sqrt{3}\Cdota6\Cdota\dfrac{1}{2} \\[4pt]
&=\dfrac{15\sqrt{3}}{2}
\end{align*}
\begin{align*}
S&=\sankaku{BCD}+\sankaku{ABD} \\[4pt]
&=\dfrac{25\sqrt{3}}{2}+\dfrac{15\sqrt{3}}{2} \\[4pt]
&=20\sqrt{3}
\end{align*}
S&=\sankaku{BCD}+\sankaku{ABD} \\[4pt]
&=\dfrac{25\sqrt{3}}{2}+\dfrac{15\sqrt{3}}{2} \\[4pt]
&=20\sqrt{3}
\end{align*}



















