大学入試数学の問題には,不等式で表された立体の体積を求める問題があります。
立体の形状がどのようなものであるかも想像できない問題もあります。
しかし立体の形状を想像しなくても,その立体の体積を求めることができることを知っておきましょう。
また,このような問題は得意な人と苦手な人が分かれやすい問題のため,得点差が大きくなる問題となる可能性が高いです。
したがって,入試では合否に直結する問題とも言えます。
あなたが受験したときに出題されたときに,解くことができれば合格に近づくはずです。
2002年 大阪府大

ヒロ
それでは次の問題を解いてみよう。
2002年 大阪府大座標空間において不等式
\begin{align*}
0\leqq x\leqq\cos z\cos2z,~~
0\leqq y\leqq x\tan z,~~0\leqq z\leqq\dfrac{\pi}{4}
\end{align*}
を満たす点P $(x,~y,~z)$ の全体からなる立体 $D$ の体積を求めよ。0\leqq x\leqq\cos z\cos2z,~~
0\leqq y\leqq x\tan z,~~0\leqq z\leqq\dfrac{\pi}{4}
\end{align*}
2002年 大阪府大の考え方と解答

ヒロ
立体の体積を求める基本的な方法は積分だね。

ヒロ
具体的には,ある平面で切ったときの切り口の面積を求めて,切断面に垂直な方向に積分すれば体積を求めることができる。

どんな平面で切れば良いのですか?

ヒロ
次のことを考えよう。
立体を切断する平面を決める方法次のポイントを考えて切断する平面を決めよう。
- $xy$ 平面,$yz$ 平面,$zx$ 平面に平行な平面
- 定数になると楽になる文字に着目
- 対称性を崩さないような文字に着目

今回の場合,$z$ が定数になれば,かなり楽になりますね。

ヒロ
そうだね。不等式で表された領域を平面 $z=t$ 上に図示することができるね。
【2002年 大阪府大の解答】
平面 $z=t~\left(0\leqq t\leqq\dfrac{\pi}{4}\right)$ で切ると,断面は
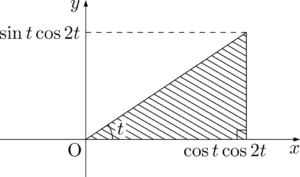
上図より断面積 $S(t)$ は
平面 $z=t~\left(0\leqq t\leqq\dfrac{\pi}{4}\right)$ で切ると,断面は
\begin{align*}
0\leqq x\leqq\cos t\cos2t,~~0\leqq y\leqq x\tan t
\end{align*}
となる。不等式が表す領域は図の斜線部分である。0\leqq x\leqq\cos t\cos2t,~~0\leqq y\leqq x\tan t
\end{align*}

上図より断面積 $S(t)$ は
\begin{align*}
S(t)&=\dfrac12\Cdota\cos t\cos2t\Cdota\sin t\cos2t \\[4pt]
&=\dfrac14\sin2t\cos^22t
\end{align*}
となる。よって,求める体積 $V$ はS(t)&=\dfrac12\Cdota\cos t\cos2t\Cdota\sin t\cos2t \\[4pt]
&=\dfrac14\sin2t\cos^22t
\end{align*}
\begin{align*}
V&=\dint{0}{\frac{\pi}{4}}S(t)\;dt \\[4pt]
&=\dint{0}{\frac{\pi}{4}}\dfrac14\sin2t\cos^22t\;dx \\[4pt]
&=\Tint{-\dfrac14\Cdota\dfrac13\Cdota\dfrac12\cos^32t}{0}{\frac{\pi}{4}} \\[4pt]
&=\dfrac{1}{24}
\end{align*}
V&=\dint{0}{\frac{\pi}{4}}S(t)\;dt \\[4pt]
&=\dint{0}{\frac{\pi}{4}}\dfrac14\sin2t\cos^22t\;dx \\[4pt]
&=\Tint{-\dfrac14\Cdota\dfrac13\Cdota\dfrac12\cos^32t}{0}{\frac{\pi}{4}} \\[4pt]
&=\dfrac{1}{24}
\end{align*}
まとめ

ヒロ
今回は平面 $z=t$ で切ることで,うまく立体の体積を求めることができた。

ヒロ
問題に応じてどの平面で切断するかをしっかり考えよう。

ヒロ
また $\dint{0}{\frac{\pi}{4}}\dfrac14\sin2t\cos^22t\;dx$ は,微分接触型の積分だから,置換せずに暗算で積分できるようにしよう。



















