係数に文字を含む3次方程式が異なる3つの実数解をもつ条件に関する問題の考え方と解法を説明します。
定数を分離することで,方程式の解の個数を2つのグラフの共有点の個数として考えることができます。ただ,定数を完全に分離すると,複雑な関数のグラフを描かなければならないことがあります。
「定数を分離する」といっても,完全に分離するのではなく,定数を含む項をまとめて分離する方法もあります。今回はその方法も解説しています。
2019年 長崎大
2019年 長崎大3次方程式 $x^3-3px+p=0$ が異なる3つの実数解をもつように,実数 $p$ の値の範囲を定めよ。
定数を分離する
【解答と考え方】
与えられた3次方程式を因数分解して実数解を具体的に求めることはできないため,定数を分離して考える。「$p=$」の形に変形することを考えると $x\neq\dfrac{1}{3}$ のとき
定数を分離するのは同じであるが,「$p=$」の形にするのではなく,$p$ を含む項を分離する。つまり
$y=3p\left(x-\dfrac{1}{3}\right)$ と変形することで,$l$ は定点 $\left(\dfrac{1}{3},~0\right)$ を通り傾き $3p$ の直線であることが分かる。
この直線 $l$ が $C$ と異なる3点と交わる状態の例を図示すると次のようになる。

$l$ と $C$ が異なる3つの共有点をもつ条件を考えるために,$l$ と $C$ が接する条件を考える。$l$ と $C$ の接点をPとし,Pの $x$ 座標を $t$ とすると,Pにおける $C$ の接線の方程式は次のようになる。
したがって,求める条件は,$p>\dfrac{1}{4}$
与えられた3次方程式を因数分解して実数解を具体的に求めることはできないため,定数を分離して考える。「$p=$」の形に変形することを考えると $x\neq\dfrac{1}{3}$ のとき
\begin{align*}
p=\dfrac{x^3}{3x-1}
\end{align*}
となることが分かる。しかし,この方針だと $y=\dfrac{x^3}{3x-1}$ のグラフを描く必要がある。また,$x=\dfrac{1}{3}$ のときも別に考えなければならない。したがって,少し考え方を変えることにする。p=\dfrac{x^3}{3x-1}
\end{align*}
定数を分離するのは同じであるが,「$p=$」の形にするのではなく,$p$ を含む項を分離する。つまり
\begin{align*}
x^3=3px-p
\end{align*}
と変形する。この変形によって,$y=x^3$ のグラフ $C$ と $y=3px-p$ のグラフ $l$ が異なる3つの共有点をもつ条件を考えることになる。x^3=3px-p
\end{align*}
$y=3p\left(x-\dfrac{1}{3}\right)$ と変形することで,$l$ は定点 $\left(\dfrac{1}{3},~0\right)$ を通り傾き $3p$ の直線であることが分かる。
この直線 $l$ が $C$ と異なる3点と交わる状態の例を図示すると次のようになる。

$l$ と $C$ が異なる3つの共有点をもつ条件を考えるために,$l$ と $C$ が接する条件を考える。$l$ と $C$ の接点をPとし,Pの $x$ 座標を $t$ とすると,Pにおける $C$ の接線の方程式は次のようになる。
\begin{align*}
&y=3t^2(x-t)+t^3 \\[4pt]
&y=3t^2x-2t^3
\end{align*}
これが $l$ と一致するから&y=3t^2(x-t)+t^3 \\[4pt]
&y=3t^2x-2t^3
\end{align*}
\begin{align*}
\begin{cases}
3t^2=3p &~\cdots\cdots① \\[4pt]
-2t^3=-p &~\cdots\cdots②
\end{cases}
\end{align*}
①,②より $p$ を消去すると\begin{cases}
3t^2=3p &~\cdots\cdots① \\[4pt]
-2t^3=-p &~\cdots\cdots②
\end{cases}
\end{align*}
\begin{align*}
&3t^2=3\Cdota2t^3 \\[4pt]
&t^2(2t-1)=0 \\[4pt]
&t=0,~\dfrac{1}{2}
\end{align*}
$t=0$ のとき,$l$ は $y=0$ となるから,$p=0$ である。また,$t=\dfrac{1}{2}$ のとき,$l$ は $y=\dfrac{3}{4}x-\dfrac{1}{4}$ となるから,$p=\dfrac{1}{4}$ である。&3t^2=3\Cdota2t^3 \\[4pt]
&t^2(2t-1)=0 \\[4pt]
&t=0,~\dfrac{1}{2}
\end{align*}
したがって,求める条件は,$p>\dfrac{1}{4}$
極値に着目する

ヒロ
定数を分離せずに考える方法を説明する。
3次方程式 $x^3-3px+p=0$ が異なる3つの実数解をもつように,実数 $p$ の値の範囲を定めよ。
【解答と考え方】
$f(x)=x^3-3px+p$ とおくと,$f(x)=0$ が異なる3つの実数解をもつのは,$y=f(x)$ のグラフが $x$ 軸と異なる3つの共有点をもつときである。
このとき,$f'(x)=0$ とすると,$x=\pm\sqrt{p}$ となるから,$f(x)$ の増減は次のようになる。
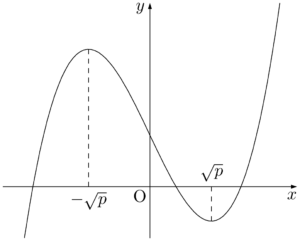
$f(x)=x^3-3px+p$ とおくと,$f(x)=0$ が異なる3つの実数解をもつのは,$y=f(x)$ のグラフが $x$ 軸と異なる3つの共有点をもつときである。
\begin{align*}
f'(x)&=3x^2-3p \\[4pt]
&=3(x^2-p)
\end{align*}
$p\leqq0$ のとき,$f'(x)\geqq0$ となり,$y=f(x)$ のグラフは単調に増加するから条件を満たさない。よって,$p>0$ である。f'(x)&=3x^2-3p \\[4pt]
&=3(x^2-p)
\end{align*}
このとき,$f'(x)=0$ とすると,$x=\pm\sqrt{p}$ となるから,$f(x)$ の増減は次のようになる。
\begin{align*}
\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & -\sqrt{p} & \cdots & \sqrt{p} & \cdots \\\hline
f'(x) & + & 0 & – & 0 & + \\\hline
f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\\hline
\end{array}
\end{align*}
条件をみたすのは,$f(-\sqrt{p})>0$ かつ $f(\sqrt{p})<0$ となるときである。\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & -\sqrt{p} & \cdots & \sqrt{p} & \cdots \\\hline
f'(x) & + & 0 & – & 0 & + \\\hline
f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\\hline
\end{array}
\end{align*}

\begin{align*} f(-\sqrt{p})&=-p\sqrt{p}+3p\sqrt{p}+p \\[4pt] &=2p\sqrt{p}+p \end{align*}
$p>0$ より,常に $f(-\sqrt{p})>0$ となる。\begin{align*}
f(\sqrt{p})&=p\sqrt{p}-3p\sqrt{p}+p \\[4pt]
&=-2p\sqrt{p}+p \\[4pt]
&=-p(2\sqrt{p}-1)<0 \end{align*}
$p>0$ よりf(\sqrt{p})&=p\sqrt{p}-3p\sqrt{p}+p \\[4pt]
&=-2p\sqrt{p}+p \\[4pt]
&=-p(2\sqrt{p}-1)<0 \end{align*}
\begin{align*}
&2\sqrt{p}-1>0 \\[4pt]
&\sqrt{p}>\dfrac{1}{2} \\[4pt]
&p>\dfrac{1}{4}
\end{align*}
よって,求める $p$ の値の範囲は,$p>\dfrac{1}{4}$&2\sqrt{p}-1>0 \\[4pt]
&\sqrt{p}>\dfrac{1}{2} \\[4pt]
&p>\dfrac{1}{4}
\end{align*}

ヒロ
ちなみに $f(-\sqrt{p})f(\sqrt{p})<0$ として解く方法もある。


















