ここでは,様々な2次関数の最大値と最小値について説明します。
2次関数の最大値と最小値を求める問題では,軸と定義域の位置関係が重要です。
様々な問題を解くことによって,2次関数の最大最小問題に慣れましょう。
最大値と最小値を求める問題

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題$2x+y+4=0$ のとき,$xy$ の最大値を求めよ。またこのときの $x$ と $y$ の値も求めよ。

ヒロ
$x$ と $y$ のどちらを消去しても良いが,$y$ を消去する方が係数が分数にならずに整数になるから計算しやすいだろう。
【考え方と解答】
$2x+y+4=0$ より $y=-2x-4$
$z=xy$ とおくと,
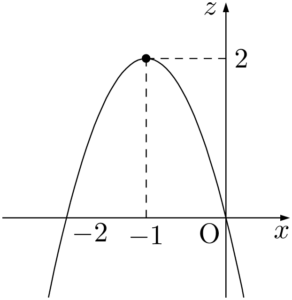
グラフより $z$ は $x=-1$ のときに最大になる。
このとき $y=2-4=-2$ である。
したがって,最大値 $2$($x=-1,~y=-2$ のとき)
$2x+y+4=0$ より $y=-2x-4$
$z=xy$ とおくと,
\begin{align*}
z&=x(-2x-4) \\[4pt]
&=-2(x+1)^2+2
\end{align*}
z&=x(-2x-4) \\[4pt]
&=-2(x+1)^2+2
\end{align*}

グラフより $z$ は $x=-1$ のときに最大になる。
このとき $y=2-4=-2$ である。
したがって,最大値 $2$($x=-1,~y=-2$ のとき)
【平方完成について】
$z=x(-2x-4)$ を平方完成するときに,次のように展開してから平方完成する人が多い。
\begin{align*}
z&=-2x^2-4x \\[4pt]
&=-2(x+1)^2+2
\end{align*}
平方完成をする方法は自由であるが,様々な方法があることを知っておこう。z&=-2x^2-4x \\[4pt]
&=-2(x+1)^2+2
\end{align*}
今回は「積の形」になっていることが都合が良い。$y=0$ となる $x$ の値が $x=0,~-2$ であることがすぐに分かる。
2次関数のグラフは放物線で,軸に関して対称であることから,軸の方程式が $x=-1$ であると分かる。つまり
\begin{align*}
y=-2(x+1)^2+\bigcirc
\end{align*}
と平方完成できる。あとは$\bigcirc$を決定するために,$y=x(-2x-4)$ 上の1点を利用すれば良い。最も簡単なのは原点だろう。y=-2(x+1)^2+\bigcirc
\end{align*}
したがって $x=0$ のときに $y=0$ となるように$\bigcirc$を決めると $\bigcirc=2$ となるから
\begin{align*}
y=-2(x+1)^2+2
\end{align*}
と平方完成することができる。y=-2(x+1)^2+2
\end{align*}
最大値と最小値を求める問題2

ヒロ
次も実際に定期テストで出題された問題。
問題$x,~y$ が $x^2+2y^2=1$ と満たすとき,$\dfrac{1}{2}x+y^2$ の最大値と最小値を求めよ。また,そのときの $x,~y$ の値を求めよ。

ヒロ
この問題も $x$ と $y$ のどちらかを消去しよう。

ヒロ
最大値と最小値を考える式の形から,$y^2$ を $x$ で表すと,$x$ の2次関数になることが分かる。

ヒロ
$x$ を $y$ で表そうとすると,根号が出てくるので $y$ の2次関数にはならない。
【考え方と解答】
$x^2+2y^2=1$ より $y^2=-\dfrac{1}{2}x^2+\dfrac{1}{2}$
$x$ の定義域が書かれていないけど,すべての実数をとるわけではないことに注意しよう。
$y^2\geqq0$ であることを考えると
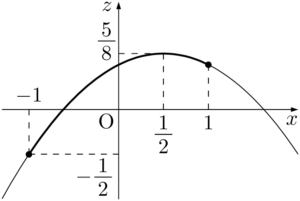
グラフより,$x=\dfrac{1}{2}$ のとき最大となり,$x=-1$ のとき最小となる。
$x=\dfrac{1}{2}$ のとき
$x=\dfrac{1}{2},~y=\pm\dfrac{\sqrt{6}}{4}$ のとき最大値 $\dfrac{5}{8}$ をとり,$x=-1,~y=0$ のとき最小値 $-\dfrac{1}{2}$ をとる。
$x^2+2y^2=1$ より $y^2=-\dfrac{1}{2}x^2+\dfrac{1}{2}$
$x$ の定義域が書かれていないけど,すべての実数をとるわけではないことに注意しよう。
$y^2\geqq0$ であることを考えると
\begin{align*}
&-\dfrac{1}{2}x^2+\dfrac{1}{2}\geqq0 \\[4pt]
&x^2\leqq1 \\[4pt]
&-1\leqq x\leqq1
\end{align*}
$z=\dfrac{1}{2}x+y^2$ とおくと&-\dfrac{1}{2}x^2+\dfrac{1}{2}\geqq0 \\[4pt]
&x^2\leqq1 \\[4pt]
&-1\leqq x\leqq1
\end{align*}
\begin{align*}
z&=\dfrac{1}{2}x-\dfrac{1}{2}x^2+\dfrac{1}{2} \\[4pt]
&=-\dfrac{1}{2}\left(x-\dfrac{1}{2}\right)^2+\dfrac{5}{8}
\end{align*}
z&=\dfrac{1}{2}x-\dfrac{1}{2}x^2+\dfrac{1}{2} \\[4pt]
&=-\dfrac{1}{2}\left(x-\dfrac{1}{2}\right)^2+\dfrac{5}{8}
\end{align*}

グラフより,$x=\dfrac{1}{2}$ のとき最大となり,$x=-1$ のとき最小となる。
$x=\dfrac{1}{2}$ のとき
\begin{align*}
&y^2=-\dfrac{1}{8}+\dfrac{1}{2}=\dfrac{3}{8} \\[4pt]
&y=\pm\dfrac{\sqrt{6}}{4}
\end{align*}
$x=-1$ のとき&y^2=-\dfrac{1}{8}+\dfrac{1}{2}=\dfrac{3}{8} \\[4pt]
&y=\pm\dfrac{\sqrt{6}}{4}
\end{align*}
\begin{align*}
&y^2=-\dfrac{1}{2}+\dfrac{1}{2}=0 \\[4pt]
&y=0
\end{align*}
以上より&y^2=-\dfrac{1}{2}+\dfrac{1}{2}=0 \\[4pt]
&y=0
\end{align*}
$x=\dfrac{1}{2},~y=\pm\dfrac{\sqrt{6}}{4}$ のとき最大値 $\dfrac{5}{8}$ をとり,$x=-1,~y=0$ のとき最小値 $-\dfrac{1}{2}$ をとる。
最大値と最小値を求める問題3

ヒロ
実際に定期テストで出題された問題をどんどん解いていこう。
問題$p$ を定数とする。関数 $y=(x^2-2x)^2+6p(x^2-2x)+3p+1$ の最小値を $p$ の式で表せ。

ヒロ
同じ式のカタマリがあることに気付こう。

ヒロ
文字を置き換えたら,その文字の定義域を確認するようにしよう。

ヒロ
置き換える前の文字の定義域がすべての実数であっても,置き換えた後の文字もすべての実数をとるとは限らないよ。
【考え方と解答】
$x^2-2x=t$ とおくと,$t=(x-1)^2-1$
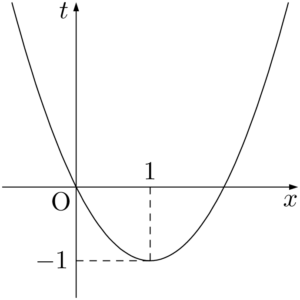
$x$ はすべての実数をとるとき,グラフより $t\geqq-1$ である。このとき
(i) $-3p\leqq-1$ すなわち $p\geqq\dfrac{1}{3}$ のとき
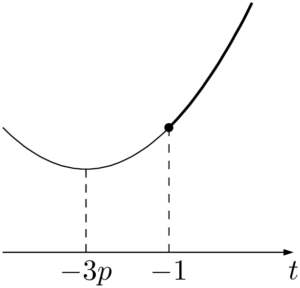
グラフより,$t=-1$ のとき最小となるから,最小値は
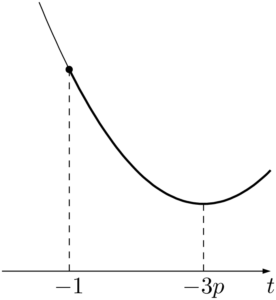
グラフより,$t=-3p$ のとき最小値 $-9p^2+3p+1$ をとる。
以上より,求める最小値は次のようになる。
$x^2-2x=t$ とおくと,$t=(x-1)^2-1$

$x$ はすべての実数をとるとき,グラフより $t\geqq-1$ である。このとき
\begin{align*}
y&=t^2+6pt+3p+1 \\[4pt]
&=(t+3p)^2-9p^2+3p+1
\end{align*}
軸 $t=-3p$ が定義域 $t\geqq-1$ に含まれるかどうかで場合分けをする。y&=t^2+6pt+3p+1 \\[4pt]
&=(t+3p)^2-9p^2+3p+1
\end{align*}
(i) $-3p\leqq-1$ すなわち $p\geqq\dfrac{1}{3}$ のとき

グラフより,$t=-1$ のとき最小となるから,最小値は
\begin{align*}
y=1-6p+3p+1=-3p+2
\end{align*}
(ii) $-1\leqq-3p$ すなわち $p\leqq\dfrac{1}{3}$ のときy=1-6p+3p+1=-3p+2
\end{align*}

グラフより,$t=-3p$ のとき最小値 $-9p^2+3p+1$ をとる。
以上より,求める最小値は次のようになる。
\begin{align*}
\begin{cases}
&p\geqq\dfrac{1}{3} のとき,-3p+2 \\[4pt]
&p\leqq\dfrac{1}{3} のとき,-9p^2+3p+1
\end{cases}
\end{align*}
\begin{cases}
&p\geqq\dfrac{1}{3} のとき,-3p+2 \\[4pt]
&p\leqq\dfrac{1}{3} のとき,-9p^2+3p+1
\end{cases}
\end{align*}
最大値と最小値を求める問題3

ヒロ
次は与えられている関数は2次関数ではないが,文字の置き換えによって2次関数の最大最小問題になる。

ヒロ
定期テストに出題された問題の中では難しい。
問題関数 $y=(x^2-6x+7)(x^2-6x-5)-8x^2+48x-42$ の最大値と最小値,およびそのときの $x$ の値を求めよ。ただし,$x$ の範囲を $0\leqq x\leqq8$ とする。

ヒロ
この問題では「$x^2-6x$」が目立つから1つの文字 $t$ で置いて考えよう。
【考え方と解答】
$x^2-6x=t$ とおくと,$t=(x-3)^2-9$
$0\leqq x\leqq8$ のとき,$t$ のグラフは次の太線部になるから,$-9\leqq t\leqq16$
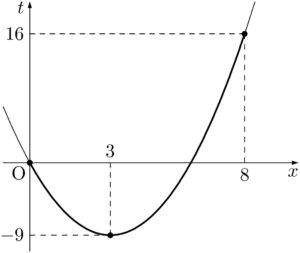
与えられた関数を $t$ を用いて表す。
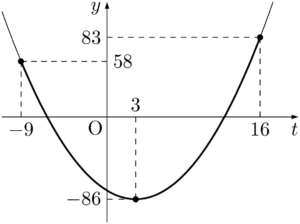
グラフより,$t=16$ のとき最大値 $83$ をとり,$t=3$ のとき最小値 $-86$ をとる。
$t=16$ のときグラフより $x=8$ である。$t=3$ のとき
したがって,
最大値 $83$($x=8$ のとき),最小値 $-86$($x=3+2\sqrt{3}$ のとき)
$x^2-6x=t$ とおくと,$t=(x-3)^2-9$
$0\leqq x\leqq8$ のとき,$t$ のグラフは次の太線部になるから,$-9\leqq t\leqq16$

与えられた関数を $t$ を用いて表す。
\begin{align*}
y&=(x^2-6x+7)(x^2-6x-5)-8x^2+48x-42 \\[4pt]
&=(t+7)(t-5)-8t-42 \\[4pt]
&=t^2-6t-77 \\[4pt]
&=(t-3)^2-86
\end{align*}
y&=(x^2-6x+7)(x^2-6x-5)-8x^2+48x-42 \\[4pt]
&=(t+7)(t-5)-8t-42 \\[4pt]
&=t^2-6t-77 \\[4pt]
&=(t-3)^2-86
\end{align*}

グラフより,$t=16$ のとき最大値 $83$ をとり,$t=3$ のとき最小値 $-86$ をとる。
$t=16$ のときグラフより $x=8$ である。$t=3$ のとき
\begin{align*}
&(x-3)^2-9=3 \\[4pt]
&(x-3)^2=12 \\[4pt]
&x-3=\pm2\sqrt{3} \\[4pt]
&x=3\pm2\sqrt{3}
\end{align*}
$0\leqq x\leqq8$ より $x=3+2\sqrt{3}$&(x-3)^2-9=3 \\[4pt]
&(x-3)^2=12 \\[4pt]
&x-3=\pm2\sqrt{3} \\[4pt]
&x=3\pm2\sqrt{3}
\end{align*}
したがって,
最大値 $83$($x=8$ のとき),最小値 $-86$($x=3+2\sqrt{3}$ のとき)


















