1998年センター試験 数学ⅡB 第1問 複素数平面

1998年センター試験数学ⅡB 第1問複素数平面の解説をします。

まだ問題を解いていない人は解いてから解説を読んでください。

1998年センターⅡB 第1問複素数平面　この問題では，複素数の偏角はすべて $0\Deg$ 以上 $360\Deg$ 未満とする。
　$\alpha=2\sqrt2(1+i)$ とし，等式

\begin{align*}
\abs{z-\alpha}=2
\end{align*}

を満たす複素数 $z$ を考える。
(1) $z$ の中で絶対値が最大となるものは

\begin{align*}
\myBox{ア}\sqrt{\myBox{イ}}\left(\myBox{ウ}+i\right)
\end{align*}

である。
(2) $z$ の中で偏角が最大となるものを $\beta$ とおくと，$\dfrac{\beta}{\alpha}$ の絶対値は $\dfrac{\sqrt{\myBox{エ}}}{\myBox{オ}}$ で，偏角は $\myBox{カキ}\Deg$ である。また

\begin{align*}
\beta=\dfrac{\myBox{ク}\sqrt{\myBox{ケ}}-\sqrt{\myBox{コ}}}{\myBox{サ}}
+\dfrac{\myBox{シ}\sqrt{\myBox{ス}}+\sqrt{\myBox{セ}}}{\myBox{ソ}}\,i
\end{align*}

である。さらに，$\beta$ の偏角は $\myBox{タチ}\Deg$ である。
　$1\leqq n\leqq100$ の範囲で，$\beta^n$ が実数になる整数 $n$ は $\myBox{ツ}$ 個ある。

Contents

1 (1)の解答
2 (2)の解答
3 1998年センター数学ⅡB 複素数平面を解いた感想

(1)の解答

ヒロ

絶対値が最大となる $z$ を求める問題。

【「絶対値が最大」の意味を考える】
$z,~\alpha$ が表す点をそれぞれ，Aとすると，
$\abs{z-\alpha}=2$ より，APの長さは2で一定であることが分かる。
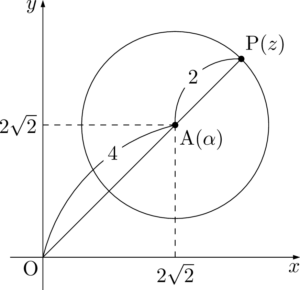
$z$ の絶対値 $\abs{z}$ はOPの長さを表すから，3点O，A，Pがこの順に一直線上に並ぶとき，$\abs{z}$ が最大になることが分かる。

【ア～ウの解答】
　$\abs{z}$ が最大になるのは，3点　$\mathrm{O}(0)$, $\mathrm{A}(\alpha)$, $\mathrm{P}(z)$ がこの順に一直線上に並ぶときである。したがって，$k$ を実数として $z=k\alpha$ と表せる。ここで

\begin{align*}
\mathrm{OA}&=\abs{\alpha} \\[4pt]
&=2\sqrt{2}\abs{1+i}=4
\end{align*}

であることを考えると，

\begin{align*}
&k\abs{\alpha}=\mathrm{OA}+\mathrm{AP} \\[4pt]
&4k=4+2 \\[4pt]
&k=\dfrac{3}{2}
\end{align*}

よって，求める複素数 $z$ は

\begin{align*}
z&=\dfrac{3}{2}\Cdota2\sqrt{2}(1+i) \\[4pt]
&=3\sqrt{2}(1+i)
\end{align*}

(2)の解答

(2) $z$ の中で偏角が最大となるものを $\beta$ とおくと，$\dfrac{\beta}{\alpha}$ の絶対値は $\dfrac{\sqrt{\myBox{エ}}}{\myBox{オ}}$ で，偏角は $\myBox{カキ}\Deg$ である。また
\begin{align*}
\beta=\dfrac{\myBox{ク}\sqrt{\myBox{ケ}}-\sqrt{\myBox{コ}}}{\myBox{サ}}
+\dfrac{\myBox{シ}\sqrt{\myBox{ス}}+\sqrt{\myBox{セ}}}{\myBox{ソ}}\,i
\end{align*}
である。さらに，$\beta$ の偏角は $\myBox{タチ}\Deg$ である。
　$1\leqq n\leqq100$ の範囲で，$\beta^n$ が実数になる整数 $n$ は $\myBox{ツ}$ 個ある。

ヒロ

次は偏角が最大になるときの $z$ を求める問題。

【「偏角が最大」の意味を考える】
$\mathrm{P}(z)$ の偏角とは，実軸とOPのなす角のことである。
したがって，偏角が最大のとき，OPは点Aを中心とする半径2の円 $C$ に接する。

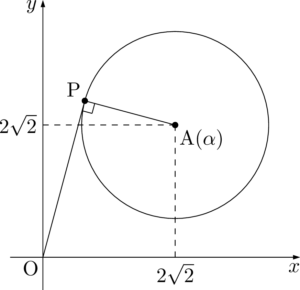
　いま求めたいものは $\dfrac{\beta}{\alpha}$ の絶対値と偏角である。絶対値については $\abs{\beta}$ を求めればよい。つまりOPの長さを求めればよい。偏角は $\kaku{AOP}$ を表しているから，$\sankaku{OAP}$ に着目すればよいことが分かる。

【エ～キの解答】
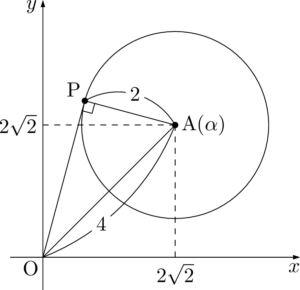
$z$ の偏角が最大になるのは，OPが円 $C$ に接するときである。
$\sankaku{OAP}$ において，$\mathrm{OA}=4$, $\mathrm{AP}=2$ より，$\sankaku{OAP}$ は $1:2:\sqrt{3}$ の三角定規の三角形であることが分かるから，

\begin{align*}
\abs{\beta}=\mathrm{OP}=2\sqrt{3}
\end{align*}

よって，

\begin{align*}
\dfrac{\beta}{\alpha}=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}
\end{align*}

また，偏角は

\begin{align*}
\arg\left(\dfrac{\beta}{\alpha}\right)&=\kaku{AOP} \\[4pt]
&=30\Deg
\end{align*}

ヒロ

次は $\beta$ を求める問題。

ヒロ

$\dfrac{\beta}{\alpha}$ の絶対値と偏角が分かっているから極形式を利用すれば良いね。

複素数の極形式複素数 $z$ の絶対値が $r~(>0)$ で，偏角が $\theta$ のとき

\begin{align*}
z=r(\cos\theta+i\sin\theta)
\end{align*}

と表される。

【ク～ソの解答】
$\dfrac{\beta}{\alpha}$ の絶対値が$\dfrac{\sqrt{3}}{2}$ で，偏角が $30\Deg$ であるから

\begin{align*}
\dfrac{\beta}{\alpha}&=\dfrac{\sqrt{3}}{2}(\cos30\Deg+i\sin30\Deg) \\[4pt]
&=\dfrac{\sqrt{3}}{2}\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \\[4pt]
&=\dfrac{3+\sqrt{3}i}{4}
\end{align*}

よって

\begin{align*}
\beta&=\dfrac{3+\sqrt{3}i}{4}\alpha \\[4pt]
&=\dfrac{3+\sqrt{3}i}{4}\Cdota2\sqrt{2}(1+i) \\[4pt]
&=\dfrac{\sqrt{2}}{2}\left\{3-\sqrt{3}+(3+\sqrt{3})i\right\} \\[4pt]
&=\dfrac{3\sqrt{2}-\sqrt{6}}{2}+\dfrac{3\sqrt{2}+\sqrt{6}}{2}i
\end{align*}

ヒロ

次は $\beta$ の偏角を求めるボーナス問題。

【タチの解答】
$\arg(\alpha)=45\Deg$ であるから，

\begin{align*}
\arg(\beta)&=45\Deg+\kaku{AOP} \\[4pt]
&=45\Deg+30\Deg=75\Deg
\end{align*}

ヒロ

最後は $\beta^n$ が実数になる整数 $n$ の個数を求める問題。

ヒロ

複素数の累乗が出てきてるので，ド・モアブルの定理を復習しておこう。

ド・モアブルの定理複素数 $z$ を極形式で表したとき，$z=r(\cos\theta+i\sin\theta)$ となるとすると，

\begin{align*}
z^n=r^n(\cos n\theta+i\sin n\theta)
\end{align*}

となる。

【複素数が実数になる条件を考える】
　複素数 $z=r(\cos\theta+i\sin\theta)$ の $n$ 乗は，ド・モアブルの定理より，絶対値は $n$ 乗になり，偏角は $n$ 倍になる。
　また，複素数が実数になるのは，偏角が $180\Deg$ の整数倍のときだから，$75n$ が180の倍数になる $n$ の個数を求めれば良いことが分かる。

【ツの解答】
　$\arg(\beta)=75\Deg$ であるから，$\beta^n$ が実数になるのは，$75n$ が180の倍数になるときである。
　$75=3\times5^2$, $180=2^2\times3^2\times5$ より，$n=2^2\times3\times(整数)$ のとき，条件を満たす。$1\leqq n\leqq100$ の範囲の12の倍数は8個であるから，求める整数 $n$ は8個ある。